Microsystems are the natural occurring building blocks that compose things. They are self-organized, dissipative structures at the microscale relative to its surrounding macrosystem. Leptons, baryons, atoms, molecules, prokaryotic cells, multi-cellular organisms, human families, and corporations are some of the primary examples of microsystems at different levels of complexity.
Since a microsystem is within a macrosystem, the death of the microsystem usually releases its components back to a lower level of complexity, so the information contained in the components will be reincorporated in the lower level. But in addition those components have a chance to be reincorporated into a different microsystem, possibly at the higher level again. What the structure of this process of reincorporation is the key question. We hypothesize this process of reincorporation is intimately related to the notions of chaos and order.
Much of the progress in understanding the interplay between chaos and order regimes has been in simplified situations at one level of complexity using mathematical modeling. It is true that deterministic (i.e., mathematical) chaos and deterministic order regimes do reflect a great deal of the properties of the natural world. However, it is fairly evident that the natural world has multiple levels of chaos and order. So are the laws the same for non-deterministic chaos and non-deterministic order? Are there any missing properties or laws that are essential in understanding the evolution of universe that involve multiple levels of complexity?
Three areas of research: chaos theory, non-equilibrium chemical thermodynamics, and artificial life have given some clues into the process of increasing complexity. The route from order to chaos has been explored by chaos theory. Non-equilibrium chemical thermodynamics [15] have shown the beginning of a route from chaos to order. In the area of artificial life, Langton [11] has hypothesized that between chaos and order there is an ``edge of chaos.'' This edge-of-chaos is where physical systems can exhibit a high degree of physical computation. Langton has asserted that at the edge-of-chaos is where complexity arises and is akin to a phase transition. Crutchfield [3,14] further argues that all physical systems can compute to some degree, and the degree of computation at an edge of chaos forms an information-rich peak, higher than the ordered or chaotic regimes. In other words, there is no distinct boundary, in the conventional sense, encompassing or demarcating an edge-of-chaos. (Note, however, that neither Langton nor Crutchfield have studied natural, massive dissipative structures using their analysis methods.)
If physical systems are performing computation by their very own dynamics, then what happens when several of these systems couple or decouple their dynamics? The dynamics of coupling most likely are related to development or growth. The dynamics of decoupling should be related to decay or death. The death of a ``complex'' of physical systems must also play a part in transfer of information between the levels of complexity.
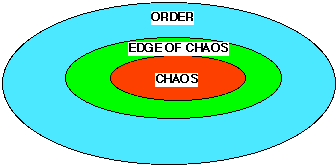
When observing vast range of the macrosystems and microsystems of our natural world, we have noticed the particular patterns of chaos, order, and the edge-of-chaos. Therefore, we hypothesize that there are three basic conceptual regimes of matter at a major level of complexity from a physical computation perspective: chaotic, ordered, and an ``edge of chaos'' as depicted in Figure 1.

The actual size of the edge-of-chaos region is very small compared to chaotic and ordered regimes. The chaotic region has most of the mass and energy, but the ordered region occupies most of the space. The chaotic region supplies the evolutionary energy for the growth of the edge-of-chaos. The order region is the ``material'' area for the storage of dynamic structures (i.e., microsystems).
The chaotic regime is where nothing can be predicted about the position
of the microsystems after a duration of time. The chaotic region is centered
at the highest physical temperature. On the other hand, the order region
is the result of the dissipation of energy and material of the chaotic
region and the debris of previous existing dissipative structures. The
order regime is where the positional state of entities repeats after a
duration of time. The edge-of-chaos regime is the phase transition between
the ordered region and the chaotic region. Our solar system is one specific
example of a dissipative system as in Figure 2.

Another view of a major level complexity is the characterization of the phases of dynamic organization of the dominant microsystems within a macrosystem. Figure 3 represents a phase space of a level of complexity.
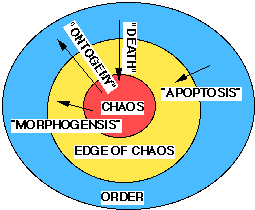
Figure 4 represents the phase space of complexity level 2. The particles the sun: protons and neutrons form the chaotic center. The nuclei and ions in sun and planets form the edge-of-chaos. The atoms of the planets, asteriods, comets, and Ort cloud compose the order region. The ``morphogenesis'' of simpler microsystems combining together into a dynamic structure represent the transition from chaos towards order via an edge-of-chaos.
The word morphogenesis is generalized to include phase transitions at
major levels of complexity including: quarks to baryon, baryons to nuclei,
ions to molecular ion, molecular autocatalyic sets to cell (e.g., procaryote
cell division), gametes to organism, parents to family, families to``societies''
(e.g., corporations). The word ``apoptosis'' is generalized to include
the phase transitions from order to chaos via an edge-of-chaos which include
nuclei to baryons(e.g. radioactive decay), atom to ion, molecule to molecular
cations/ions (e.g. chemical decomposition), cell to molecular sets, organism
to cells (e.g., molting), family to organisms (e.g., divorce), ``societies''
to families (e.g. corporate restructuring).
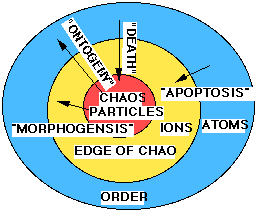
At the next level of major complexity above atoms is the transition
from atoms to molecules. Planetary systems are the typical massive dissipative
structure in creating more complex molecules (microsystems). Figure 5 illustrates
the major complexity level three. For example, the earth's center is a
center for atomic chaos. The nuclei in the center of earth are relatively
stable, but too hot to form molecules in the conventional sense. The planet's
crust is an edge-of-chaos, where atomic ions can combine or decompose into.
The planet's atmosphere and planetary space are the order region, where
relative numbers and types of molecules such as oxygen and hydrocarbons
are relatively stable compared to the surface.
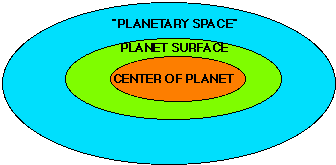
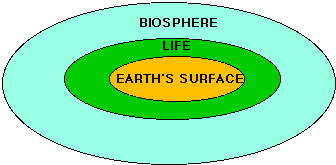
The planet's biosphere (Gaia) is the next level of major complexity
(as in Figure 6), where molecules combine to make cells. The planet surface
is the chaotic center. The individual molecules are chaotic in the long
run. The edge-of-chaos region is composed of the autocatalytic sets of
molecules that are involved in life at the moment. The order region are
all the life-based organic molecules in the biosphere.
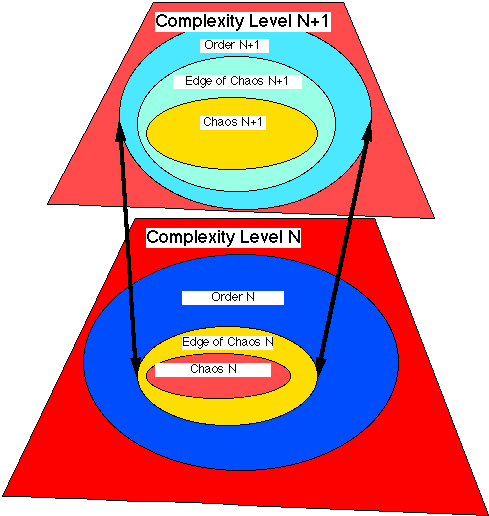
We hypothesize that all massive dissipative structures have an edge-of-chaos as in lofc. (Although the actual size of the edge-of-chaos is extremely small compared to the chaotic and order regions.) If a further set of conditions exist, an edge-of-chaos within a dissipative structure can be substantial in absolute terms (but not relative) and contain another major level of complexity. Figure 7 illustrates the embedding of one major complexity level within another.
Within an edge-of-chaos region there can be multiple levels of major complexity. If an edge-of-chaos region (level N) is large, the underlying stable microsystems (level N) are diverse in type, and the chaos region (level N) of the surrounding dissipative structure is stable, then the next level of major complexity (level N+1) can form. In the next level of major complexity (level N+1), there is a chaotic region (level N+1), an order region (level N+1), and an edge of chaos (level N+1).
In the natural world, galaxies, star systems with planets, and the earth are the most readily observable examples of massive dissipative structures with multiple levels of complexity. There are also higher-level dissipative structures that have been hypothesized, such as Gaia [12], Hypersea (``organismal entity'' that extended life onto land) [13], and Metaman (global mankind with electronic communication as ``organismal entity'') [19] that will be useful in understanding the evolution of complexity.
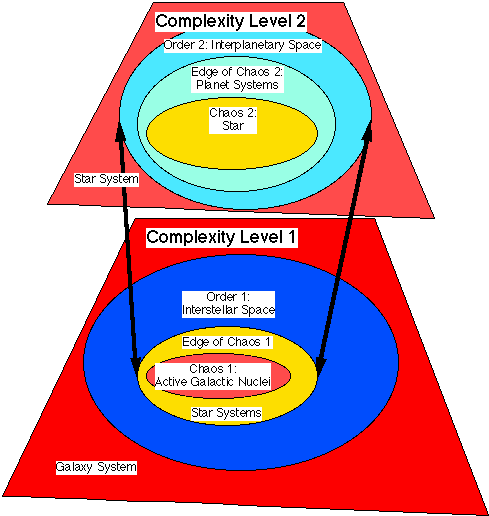
In more concrete terms as in Figure 8, for example, the star systems
in the middle periphery of Milky Way galaxy is a large region, the underlying
charged particles are diverse enough to form nuclei. The center of galaxy
has a black hole which serves as a chaotic center (level 1). The interaction
of living star systems, the dynamic debris of the dead star systems, and
the formation of our solar system create a part of an edge-of-chaos (level
1) in our galaxy. Our solar system is on the edge-of-chaos (level 1) and
comprises of a stable chaotic region (level 2), our sun, and the order
region (level 2), namely interplanetary space and the Ort cloud. The edge-of-chaos
(level 2) are the geologically active planets and moons of the solar system.
Although in a natural chaotic regime, the position of microsystems cannot be predicted after a certain amount of time, the microsystems themselves are mostly stable and hence predictable. There is ``order within chaos''. For example, our sun is chaotic relative to atoms (atomic nuclei with a complete set of electrons), but is relatively stable for particles. Within the sun, the number of protons, neutrons, and electrons is statistically stable. Also, relatively stable within the sun are the nuclei that were included in the matter coalesced by the sun from the debris of previous deaths of stars. (Whereas, nuclei are not preserved in within a black hole, which is a dissipative structure at a lower level of major complexity.) On the other hand, any matter, such as an asteroid in the form of atoms, molecules, or anything more complex that is incorporated into the sun is reduced to the complexity of atomic ions.
In the order regime, the position of the microsystem can be predicted to a degree. But, within an order regime there can be some chaos, depending on the degree of symmetry breaking and bifurcation of microsystems. For example, in the solar system, most of the matter in interplanetary space and the Ort cloud is in the form of atoms and is frozen and relatively inactive. However, the microsystems in the order regime themselves although mostly stable, there is no predictability in the sudden death of any particular microsystem. (For example, a neutrino colliding with a proton can start the destruction). There is ``chaos within order''. Because of this ultimate instability of it's component microsystems, no order regime is completely ordered. In addition, an order regime is physically next to a chaotic regime, which subjects the order region to the energy fluctuations of the chaotic region.
Between chaos and order, within an edge-of-chaos there can be multiple levels of complexity. Growth is the generic word for indicating the process of going from chaos to order. Whereas, death is the generic word for indicating the process of going from order to chaos. The feedback of the chaos and the order regions into the edge-of-chaos drive an edge-of-chaos to higher complexity.
Figure 9 illustrates the possible current path of macrosystems in the evolution of complexity in our human existence: hence called involution.
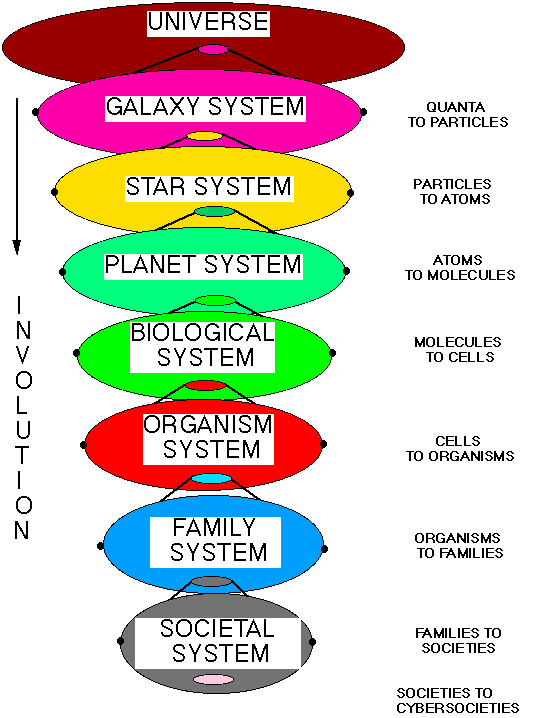
When a macrosystem (e.g., the earth) contains higher-level complexity, not only will it exhibit the processes of lower complexity, most notably, thermodynamic dissipation, but the macrosystem also will exhibit higher forms of process order, such as non-equilibrium chemical thermodynamics.
Is there any structure and process to this evolution in the higher levels of complexity? Unfortunately, the standard use the concept of ``evolution'' has been overused and includes two significantly different processes. The first process is adaptation. Algae are said to evolve or ``adapt'' as time progresses, even though they do not change in significant complexity. When one talks of the evolution of algae from their creation to the current age, there is very little implication of increasing complexity. But on other hand, the other significant process of evolution is increasing of complexity. It is generally accepted that some common ancestors of prokaryotes had evolved into multi-celled eukaryotes by the processes involving parasites, symbioses, and epigenetic programs of the genomes. This type of evolution is an increase in complexity. Stephen Jay Gould argues that the evolving to more complex organisms is only one strategy in adapting to the environment, which is true; however, there is more to the story of the evolution of complexity besides multi-cellular organisms.