The Relations between Replication and Dissipation regarding Life and Existence
(under evolution)
David M. Keirsey
R&D Intelligent Systems
Abstract
The relations between replication and dissipation are complex, for the combination in the most abstract form, I hypothesize, forms Existence. These relations, as instantiated as precise metaphors similar to the spirit of Robert Rosen’s {M,R} formalism (Rosen, 1958), form a basis for constructing models and answering difficult questions about existence and life. In particular, these relationships start to answer the question of “what is life?” in terms of specific kinds and degrees of replication and dissipation.
Keywords: replication, dissipation, life, existence, modeling
It was the best of times and worst of times -- Dickens
Introduction
Ilya Prigogine (Prigogine, 1984)(Prigogine, 1997) has put forward that dissipative structures do not obey Boltzmann's order principle, because a dissipative structure is not in equilibrium. Moreover, one must admit that the universe is not in equilibrium, it is forever changing: "evolving" as it were. This observation is key to understanding how the "evolution" of our universe and its embedded structures will proceed. The century old hypothesis of "heat death" of the universe, based on the second law of thermodynamics is no longer the most reasonable scenario because it appears that the universe is a non-equilibrium structure (Smolin, 1997). It is posited that in reality (e.g., our universe), replication and dissipation cannot be separated: one implies the other. Replication is dissipation of order, and dissipation is replication of disorder (chaos). In the Hegelian tradition, order implies disorder and disorder implies order. Replication and dissipation are entangled in any part of existence.
The second law of thermodynamics, although considered applicable to all situations (it is considered a law), it is in reality, a misleading characterization when viewed in non-equilibrium contexts. One does not have to view systems strictly in terms of linear and equilibrium contexts as physics has done for about 150 years. Construction and deconstruction are active non-linear processes that form the same discrete/continuum of bosons, fermions, particles, atoms, molecules, cells, organisms, families, societies, and cybersocieties as various forms of material replication and dissipation. Any kind of equilibrium must assume some form of entangled replication and dissipation. By definition, existence, which the abstract form of equilibrium, is the balance between replication and dissipation.
The integrating precise metaphor: replication and dissipation
There are different kinds and degrees of replication and dissipation, so the there can be a large amount of specific relations between the two depending on the specifics of what is dissipated and replicated within, through out, out of, the entity in question. However, the relation between the two processes in the "pure abstract" is simple.
Replication can be viewed as a form of dissipation, and dissipation can be viewed as a form of replication. Another way of characterizing replication in terms of the notion of "self" is as positive feedback, and characterization of dissipation of "self" is as negative feedback. Pure quantitative dissipation can be modeled by the equation: lim(ex), as x -> negative infinity. Pure quantitative replication can be modeled by lim(ex), as x -> infinity. Both pure dissipation and replication implies an infinite amount of information. Perfectly balanced pure quantitative replication and pure quantitative dissipation, which can be defined as pure quantitative equilibrium, can be modeled as lim(ex), as x -> 0. Pure quantitative equilibrium (1) implies an infinite amount of nothing, depending on the kind of thing x represents (such as Cayley numbers or a variable of higher or lower dimensions). To model quantitatively "something" in "time" one can entangle some quantitative notions of "time" via integration.
The next view of this perspective must address the question, “what is self?” Since the word “self” is a reflexive construct, the question is improper in general, but useful. For simple constructs, such as neutrinos or bosons, one has to consider the entire universe, but for more complex constructs, such as particles (e.g., hadrons), molecules, or organisms, one typically regards the material levels of complexity below the entity as equilibrium contexts and proceed to do the analysis at the major material level of complexity that that entity exists at. This scientific reductionism begs the question in general, since the properties of “self” (whatever that is) are extremely entangled with the entity and its context. In regards to life and non-life, what of “self” is replicated and what of “self” is dissipated and how, the question becomes problematic in the extreme. Oxymoronic constructs such as “self-organization,” “self-regulation,” may be nice phrases and metaphors, but they don’t have any rigorous or precise meaning. Moreover, the notion of "self-replication" cannot be true and is a confusing term.
Consider a simplest form of replication and dissipation in the abstract: a computation with the operator NAND. The table of the operator is the following.
A op B | C
-------------
1 ~a 1 | 0
1 ~a 0 | 1
0 ~a 1 | 1
0 ~a 0 | 1
Figure 1. The NAND operator
In applying the NAND operator, one kind of “replication” is seen by the situation of line 2 and 3, when only one of the inputs is a 1, which makes the output a 1 also. In this case the replication is through time. At the same time, the operation is also one kind of “dissipation” in that only looking at the output, information is lost, and one cannot recover which input was 1. In this case the dissipation is also through time. The complete analysis of the NAND operator, in terms of dissipation and replication is more complex, and what the bits represent, of course, play a factor of what is “replicative” and what is “dissipative;” nevertheless, any kind of operation or action in the real world must be both replicative and dissipative. The issue is what is "self"; the problem being "self" is another word for the concept of "self"-reference (notice the circularity of definition).
In reality, dissipation of "something" called "self" cannot be "completely" random or ordered. Let us call the first "real" dissipation as S-dissipation. S-dissipation is the death of state, which implies the form of dissipation of space, call it S-space. S-dissipation implies a primitive non-existence, which in turn, implies a primitive existence.
In reality, replication of "something" called "self" cannot be "completely" random or ordered. So let us call the first "real" replication as S-replication. S-replication is the creation of state, which implies the form of dissipation of time, call it S-time. S-replication implies primitive existence, which implies a primitive non-existence.
Since S-replication is real to a degree, the issue is how is S-time dissipated? One way S-time is dissipated is by having things that die. How do things die? By dissipating back to some kind of randomness, the S-space. But the randomness implies some kind of order. Therefore, one way to look at the notion of state is as a counting of dissipators and replicators.
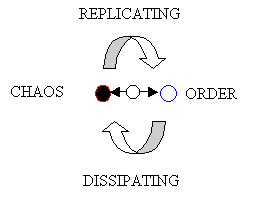 |
Figure 2. The Replication/Dissipation Metaphor
In reality, replication and dissipation are entangled, for there is no such thing as pure replication or pure dissipation. Any form of replication implies a form of dissipation and visa versa. What is major difference between replication and dissipation in the non-pure abstract? Given that replication is dissipation of order, and dissipation is replication of disorder, what does this imply? Given that any "order" must be instantiated in terms of a "measure", this implies that at least one "dimension" exists. At a minimum, replication must dissipate order along one dimension in some degree. What does "dissipate along one dimension in some degree” mean. Essentially this is a construction of the dimension into a configuration. Obviously many kinds of replication may involve dissipation of order along several dimensions or the beefing up of a dimension. Given dissipation is the opposite of replication, then it stands to reason that dissipation must replicate disorder in at least one dimension in some degree. What does "replicate disorder in at least one dimension" mean? Essentially this means a destruction of a dimension into a configuration. Obviously many kinds of dissipation may involve replication of disorder along several dimensions or partial diminution of one. Therefore in the abstract, the relationship between replication and dissipation is relation between construction and destruction of dimensions into a different configuration. The creation and destruction of dimensions must involve entanglement between dimensions, and the first set of "dimensions" that mediate other "dimensions" must include a notion of "time" (time0) which is "pure dissipation" and "space" (space0) which "pure replication". The time0 "dimension" is not a conventional dimension in that it isn't reversible, since it must be "pure dissipative" (unreal). Likewise space0 "dimension" is not a conventional dimension in that it acts like "pure replication" an infinite set of dimensions, not being specific in the any "dimension". There are few simple models that mimic some of the behavior of these dimensions: names of these models include "zero," "infinity," "negative infinity."
The description of Dissipative/Replicative processes is in the context of a global Dissipative/Replicative structure (the so-called multiverse), but at the most primitive level, one cannot talk about what it is constituted of. One must posit almost complete randomness and almost complete order as the context, but the form must have the property of dissipation and replication.
Darwin’s metaphor: evolution
Darwin’s evolutionary metaphor is an essentially a near-equilibrium model. It is simpler than the above metaphor and uses the word reproduction rather than replication and it does not emphasize the words metabolism or “natural selection” as a form of dissipation. Lastly, “mutations” just happen. One might model the general Darwinian metaphor as the following.
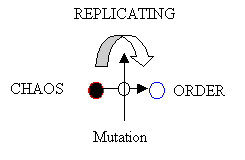 |
Figure 3. A Model of Darwinian Evolution
There are other uses of the word “evolution.” The most common use of the word evolution refers to Darwin’s model of how life changes. Darwinian evolution, which assumes “reproduction” and “metabolism” and typically is only discussed in terms of the multicellular organism part of life, is a particular model of how things change. On the other hand, the word evolution is also used when refering to changes in the universe, such as the birth and death of stars and the changing of galaxies. Higher forms of “evolution,” that is, when talking about human social change, there is a reluctance to view it in a “Darwinian” light because of the political overtones. Lastly, “evolution” in any context is rather ambiguous, because it sometimes is meant to include “progress” or in other cases, is meant to be devoid of “progress.”
The word “devolution” although not used extensively in science captures the essence of “decay,” in a vague evolutionary sense. In reality, equilibrium, is in some sense, is another way of viewing “decay” or “devolution,” or in Prigogine’s words, a kind of death. The ultimate “death” is going back into randomness, where complete randomness is the “real” death. With levels of complexity, a death is just reorganization down to an underlying material complexity.
Clausius’s Metaphor: entropy
The other major scientific metaphor, in some sense opposite of evolution, is the second law of thermodynamics. It is asserted that it governs all of matter; however, this metaphor assumes an “isolated” or “closed” system, which cannot be the case with the universe – the universe is not in equilibrium. In fact, pure equilibrium does not exist – all “equilibriums” must be dynamic, or in some metaphoric sense, living. Clausius’s metaphor is in reality a model of death and decay. A simplified model of entropy is the following:
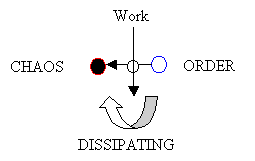 |
Figure 4. A Model of Clausius’s Entropy
Syntactically there is very little difference between the two metaphors, entropy and evolution – they are simple models, to a degree mirror images of each other. So a more complete metaphor would be to combine the two models of Clausius and Darwin to form a replicative/dissipative structure.
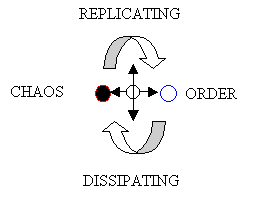 |
Figure 5: Unification of Darwin’s and Clausius’s Metaphors
This model can be applied to itself, thus creating multiple levels of complexity – roughly, there can be an evolution of complexity.
Hence, I will use the two words: involution and envolution, as semi-neologisms, to refer to the “evolution of complexity” but in the wider context of both life and non-life including the changing of: bosons and the universe, to eucaryotic multicellular life and Gaia, to cyberentities and the Web. “Involution” is the evolution of material (structure) complexity. “Envolution” is the evolution of functional complexity. Both involution and envolution are entangled, for if there is no structure, then there is no function, but also if there is no function, then there is no structure.
The relationship between dissipation and replication is examined from both a functional complexity and material complexity point of view. A “replicative/dissipative” structure is the material metaphor for naming the entity involved in the complexity, but recognizing the fact there is always a context that surrounds the entity. There is a discrete continuum from non-life to life in the “involution” and “envolution” of existence.
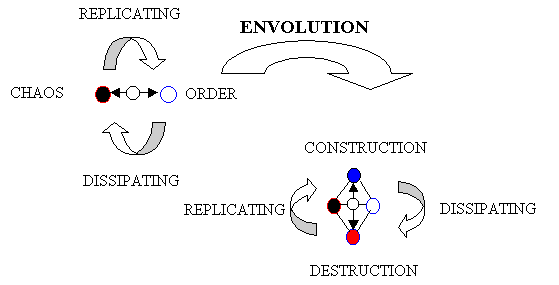 |
Figure 6. Two-levels of Functional Complexity: Envolution
The Metaphor of Problem Solving of Dissipation and Replication: Envolution
The metaphor of problem solving is used to delineate the process structure of existence. The envolution of a dissipative/replicative structure depends on the "information" of context and "information" contained in the structure, itself, and the exchange of information between the context and structure, and the transformation of "information" within the structure. The context must assumed to be a dissipative/replicative structure at a lower level of complexity. A dissipative/replicative structure has three "methods" (processes: ways of communication) for "solving" the problem of dissipation/replication. Dissipation/replication can be solved by distribution in 1) "energy," 2) "time&structure," or 3) "space."
The description of Dissipative/Replicative processes is in the context of a global Dissipative/Replicative structure (the so-called multiverse), but at the most primitive level, one cannot talk about what this multiverse is constituted of. One must posit almost complete randomness and almost complete order as the context, but the form must have the property of dissipation and replication. The following table indicates some preliminary functional roles that each level of envolution may serve in our overall envolution.
|
Envolution Metaphors for Functional Complexity |
|
Complexity 0: Multiverse vs Universe: The Problem of Existence and Non-Existence (what to exist => material systems: macro dissipation, micro replication) |
|
Complexity 1: Universe vs Galaxy Systems: The Problem of Dissipation and Replication (how to dissipate and how to replicate = time, energy versus space, matter) |
|
Complexity 2: Galaxy Systems vs Star Systems: The Problem of Stability and Instability (what to make(replicate) stable and what not to make(dissipate) stable) |
|
Complexity 3: Star Systems vs Planet Systems: The Problem of Control and Non-Control (what to control (replicate) and what not to control (dissipate)) |
|
Complexity 4: Planet Systems vs Gaia: The Problem of Inheritance and Non-inheritance (what to inherit (replicate) and what not to inherit (dissipate)) |
|
Complexity 5: Gaia vs Hypersea: The Problem of Mortality (what to live somatically (replicate) and what to die somatically (dissipate)) |
|
Complexity 6: Hypersea vs Metaman: The Problem of Knowledge (what to know (replicate) and what not to know (dissipate)) |
|
Complexity 7: Metaman vs Cybersocieties: The Problem of Learning (what to learn (replicate) and what not to learn (dissipate)) |
On the other hand, specific order (and chaos) have levels of both material and functional complexity. Another metaphor, the process structure, for material complexity will be used to explicate the involution of our universe.
The Process Structure Metaphor, A Dissipative/Replicative Structure: Involution
The following is a defining the basic structure of material complexity so to give an overarching context. Three basic regimes within a dissipative/replicative structure in terms of material complexity have been defined: chaos, order, and the edge-of-chaos/edge-of-order.
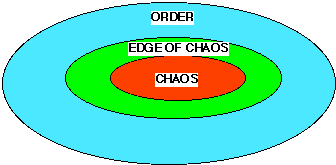 |
Figure 7. A
Dissipative/Replicative Structure: A Macrosystem
The edge-of-chaos metaphor and it associated mathematical and computational methods Mitchell (1994), and Langton (1990) is useful in describing massive dissipative/replicative structures. Every massive dissipative/replicative structure is on some edge-of-chaos, and some structures are part of multiple levels of edge-of-chaos. A large part of the edge-of-chaos metaphor involves both a macro-process and a macro-structure. But also it includes micro-structures and micro-processes. The combination of macro-process, macro-structure, micro-processes, and micro-structures will be the basis for the metaphor.
The edge-of-order metaphor is a new metaphor borrowed from the edge-of-chaos metaphor, to make crucial link to the other important metaphor of replication and link it to the notion of life, which also applies to non-life phenomena. It is important to realize the edge-of-order is the same as the edge-of-chaos, but viewed from a different point of view. For Darwin's metaphor of evolution can be applied to non-life systems, because some kind of replication exists in these systems.

Figure 8. Replication and Dissipation: Involution
The material complexity of the universe can viewed as a processes of successive layers of chaos, order, and the edge of chaos: involution. Within the edge-of-chaos/order there can be another level of material complexity.
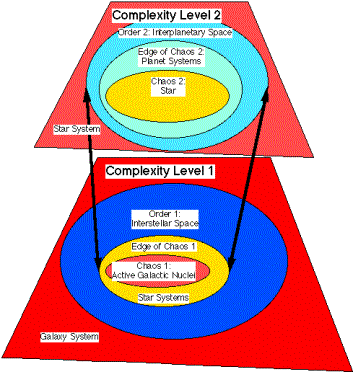 |
Figure 9. Two-levels of Major Material Complexity: Involution
Abstractly, each level of complexity has three basic regions as depicted in Figures 7 and 8: the chaotic region, the order region, and the edge between the chaotic and order region. Figures 7 and 8 depict the major levels of material complexity 1& 2 in terms of these three regions. The chaotic region of a level of complexity supplies the evolutionary energy for the growth of an "edge of chaos" for the next level of complexity. The order region is the "material" area for storage of dynamic structures that were created by the process at the edge of chaos. The order region largely preserves the information at a level of complexity in these dynamic structures. But in addition, these structures in the order region can be fed back into the edge of chaos by energy fluctuations created by the turbulence of the chaotic region into the dynamic structures of the order region.
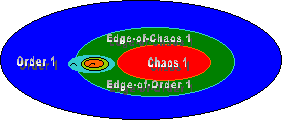 |
Figure 10. Two level Involution
Another simple metaphor to visualize the level of complexity, is view each level centered on a conceptual form of equilibrium in time and space, even though there is no such thing as an equilibrium in reality. The massive equilibrium, which is not exactly in equilibrium replicates and dissipates from that time and space center.
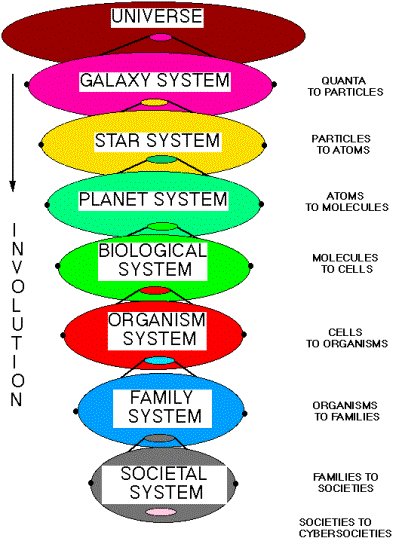 |
Figure 11. Our Involution in the Universe
Integrating life and non-life: Newton, Darwin, Boltzmann, Prigogine, and Rosen
The process structure metaphor is a metaphor that uses the combined notions of process and structure as the two equal metaphors to characterize existence. Process implies functional properties and structure implies material properties. The process structure metaphor uses both dissipation and replication.
The first phenomenological issue of dissipative/replicative structures is the realization that there is no such thing as a “closed" physical system. Even though physics has made significant progress by modeling closed systems (using the notion of equilibrium or near equilibrium), it no longer works when modeling complex systems (Bohm, 1993). And I assert all natural systems are complex systems. So, every dissipative/replicative structure (a model of a natural system), by definition, must have a context. Of course, there is the problem with infinite digression, so eventually, the overall context must be assumed. But the assumptions of this context cannot be in the form "closed". That is, one cannot do as Newton stated "Hypotheses non fingo" (I feign no hypotheses). The "meta-universe" context of our universe must be a dissipative/replicative structure in form, but the underlying process mechanisms and defining structures will probably never be known for sure. Process Physics (Cahill, 2000) appears to be the closest form of modeling the meta-universe.
The second part of the first phenomenological issue is what kind of context is the massive dissipative/replicative structure in. Clearly, if the dissipative/replicative structure is growing or shrinking, then the structure is either growing or shrinking because of itself, or the surrounding context is adding or subtracting to the process-structure. It is important to connect, at some level of abstraction, a particular structure within the total context, that is, the universe, both in material and functional terms.
The singular attribute about the involution of material systems has been that those entities physically include more and more “parts” and more importantly “components,” where a component is a functional part. There is no 1-1 correspondence between a material part and functional part (component).
In some sense the metaphor of the marketplace can be found to be useful in talking about both the internal and external functions of these components. Consider a primary molecule in involved life, for example, adenine tri-phosphate (ATP), where it serves as a marketplace for the material parts “electrons,” (leptons). The ATP molecule has multiple functions and the numerous electrons (parts) serve many different functions (as components), some being primarily dissipative, others being primarily replicative, others being primarily stabilizers (as in equilibrium). Of course those material parts exchange function constantly and rapidly in the marketplace of the molecule. One can easily view the “molecule” marketplace at a higher level of material complexity when talking about large, complex polymers such as proteins and nucleic acids. These material parts at this level of complexity are cations, ions, and monomers. The marketplace of molecular components, such as primary dissipators, in the cell is even more diverse than in the organic (molecular) world of Gaia.
In particular, life is a functional response to a kind of complex material dissipation, and since replication is entangled with dissipation, life's replicative ability is a result of a kind of material dissipation. On the other hand, life as commonly known, has several levels of material and functional complexity below it, in it, and above it, so the function of “life” and specific forms of “life,” such as mankind, have a significant number of functions besides simple replication and dissipation.
The problems and solutions of the functions: existence and non-existence, replication and dissipation, stability and non-stability, control and non-control, inheritance and non-heritance, somatic life and death, knowledge and ignorance, learning and stupidity will in the future serve as a general backdrop in understanding the functions of various forms of life. The ability to make these functional notions precisely, but abstractly, when relating to specific material entities and their context in their life cycles is the next step.
References and Bibliography
Bohm, D. and Hiley, B.J. (1993). The Undivided Universe, Routledge.
Cahill, R. (2000) Process Physics: Modelling Reality as Self-Organizing Information, The Physicist, Vol. 37(6), 191-195.
Gold, T., (1999) The Deep Hot Biosphere, Copernicus Books.
Gould, S. J., (1990) Its a Wonderful Life: The Burgess Shale and the Nature of History, Norton & Company.
Gould, S. J., (2002) The Structure of Evolutionary Theory, Belnap Publishers.
Kaufmann, S., (1996), At Home in the Universe, Oxford University Press.
Keirsey, D., (2004), The Relations between Replication and Dissipation, Proceedings of 29th International System Science Society.
Keirsey, D., (2000) Towards the Phenomenology of Massive Dissipative Structures, Intelligent Engineering Systems Through Artificial Neural Networks, Vol. 10, pp 519-524, ASME Series Press.
Keirsey, D., (1997) Toward the Physics of "Death," presented at International Conference on Complex Systems, Nashua, NH.
Keirsey, D., (1995) Involution: The Structure and Process of Existence, presented at International Conference on Complexity: Einstein Meets Magritte, Brussels, Belgium.
Langton, C., (1990) "Computation at the Edge of Chaos, Phase Transitions and Emergent Computation'', Physica D, 4, pages 12-37.
Lovelock, J., (1987) Gaia : A New Look at Life on Earth, Oxford University Press.
Margulis, L. and Sagan, D., (1997) Microcosmos: Four Billion Years of Evolution from Our Microbial Ancestors, University of California Press.
Mitchell, M., Crutchfield, J. and Hraber, D., (1994) “Dynamics, Computation, and the Edge of Chaos: A Re-Examination,” G. Cowan, D. Pines, and D. Melzner (editors), Integrative Themes, Santa Fe Institute Studies in the Sciences of Complexity, Proceedings Volume 19. Reading, MA
Margulis, L. and Sagan D., (2002) Acquiring Genomes: A Theory of the Origins of Species, Perseus Books.
McMenamin, M., and McMenamin, D., (1994) Hypersea: Life on Land, Columbia University Press.
Oyama, Susan, (1986) The Ontogeny of Information: Developmental Systems and Evolution, Cambridge Press.
Prigogine, Ilya and Isabela Stengers, (1984) Order out of Chaos: Man's New Dialog with Nature , Bantam Books.
Prigogine, Ilya and Isabela Stengers, (1997) The End of Certainity, Time, Chaos, the New Laws of Nature , Free Press.
Rosen, R., (1958) A relational theory of biological systems, Bull. Math. Biophys. 20:245-260
Rosen, R., (1978) Fundamentals of Measurement, Elsevier North-Holland.
Rosen, R., (1985) Anticipatory Systems, Pergamon Press.
Rosen, R., (1991) Life Itself, Columbia University Press.
Smolin, L., (1997) The Life of the Cosmos, Oxford University Press.
Stock, G., (1993) MetaMan, Simon and Schuster.