
S1 -> S1x{0}
->
D1
->
D1x{0} -> S2
S1= unit circle
D1= unit disk
S2= unit sphere
T2 = E2+M2+S2
E2 = M2+S2
T2 = E2+M2
T2 = S2, T2 = S2+S2
T="time", E="energy", M="mass", S="space"
 |
 |
"Disk to Sphere using Quotient Space" by Subh83 - Own work. Licensed under CC BY 3.0 via Commons.
S1 -> S1x{0} S1= unit circle |
 T2 = E2+M2+S2 E2 = M2+S2 T2 = E2+M2 T2 = S2, T2 = S2+S2 T="time", E="energy", M="mass", S="space"
|
Formal Context
Conformal Context
SubFormal Context
David M. Keirsey
(evolving e-article)
Abstract:
Using systematic analysis of phenomena across levels of complexity of existence enables a clearer understanding of the underlying structure and evolutionary process of the universe. The concept of major levels of complexity provides a framework for explaining the interaction between two adjoining levels of major complexity. This interaction is a form of information feedback. This feedback is analogous to biological evolution but appears in simpler levels of complexity that do not involve life. In addition, at higher levels of complexity, the feedback is at multiple levels thus adding to the confusion of the evolutionary mechanisms and function of life. The precise but abstract metaphorical concepts of birth, growth, equilibrium, decay, and death are shown to be fundamental processes that necessary at all levels of increasing complexity. By comparing and contrasting the levels of material and functional complexity using the rigorous methods of Relational Science and Comparative Complexity, similar to a combination of two different methodologies introduced and used by Robert Rosen and Dr. David West Keirsey, we can understand the structure and process of existence. The word involution, redefined and refined, is used to represent the process and structure of existence which creates this increasing material complexity. The word envolution, created and defined, is used to represent the process and structure of this increasing functional complexity. A rigorous semantic analysis and synthesis, Hegelian and number theoretic in nature, combined with disciplined abstract mathematical methodology similar to category theory will serve as foundation for the discovery and fabrication of useful scientific models.
The first problem in explaining the diversity is to categorize it, so as to be able to distinguish or differentiate the "things" in the universe so as to be able to use these distinctions in the discourse of reason. This has been the task of science since the Greek philosophers of antiquity started trying to objectively analyze the world. However, the major problem in science has been dealing with the "complexity" of nature[1].
There are many different complex phenomena in each field of science. Until now it has been difficult to compare phenomena between fields of science, such as physics, chemistry, biology, anthropology, and economics, in a systematic manner because it has appeared that the properties and processes of these phenomena are radically different. On the other hand, there seems to be some vague similarity between radically different phenomena of universe, such the evolution of stars and planets to the evolution of life. Indeed, the science of complexity [2][3][4] is beginning to shed some light on this similarity, and it appears there is some important commonalty between the sciences. A building of this commonalty in terms of a scientific theory could profoundly change our understanding of all the sciences and ultimately our understanding of the universe. Yet, communication between different sciences in regards to this fundamental commonalty at best at its beginnings. Scientists from different fields have difficulty in communication because they view their scientific fields as very different and effectively they speak different "languages." Nevertheless in terms of this new scientific world view, a building of a commonalty now seems possible because each field of science has a great deal of knowledge accumulated and can serve as a solid basis that can be used to analyze analogous phenomena.
In understanding the structure and process of the universe there are three important descriptive parts to the analysis in terms of the science of complexity. First part of the descriptive analysis is the naming and defining of each level of complexity of existence. This is an ambitious task, but in the process of trying to delineate and define each level, a better understanding of the fundamental commonalties between all levels will occur. In defining the levels, we must first characterize what it a level of complexity means and how one can recognize it. In this paper, the notion of major levels of complexity is introduced and used to provide an initial framework for understanding the information feedback between the major levels in time as the universe evolves.
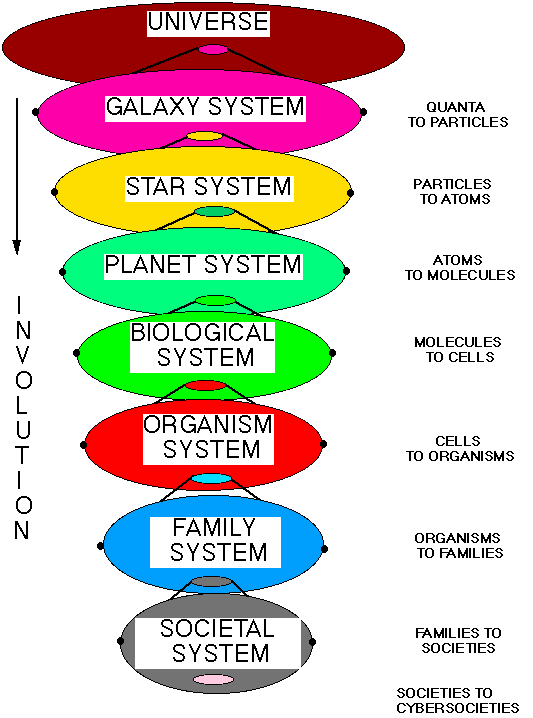
Table 1 illustrates what are the major complexity of material levels that should serve as the currently understood levels. In addition, there are successive minor levels of complexity that are between the major levels but are harder to define and discover because the evolutionary process destroys a great deal of the evidence. These basic levels can be refered to by the phrase "Material" systems, a term which has used by Robert Rosen to a significant degree. The major point about these material systems is they exist. The issue to be address in this essay is to answer the teleological question of WHY do they exist. This type of question, is not normally in the provence of science. However, many of these why questions, although not all, can be answered, in a scientific manner.
The second part of the descriptive analysis is the process description of each level of complexity. In this process description, it is important to show the commonalty between levels. This common process description, hereby called involution, will represent the common theory on how levels of complexity arise and what is the underlying structure and process of the universe. For starters there seems to be four basic processes. The analogous notions of birth, growth, decay, and death appear to common to all levels of complexity from galaxies and stars to human society and cyberspace. For example, it appears that catalysts in chemistry has a similar role of birth as genomes have in biology, and as memes have in sociology. Mapping seemly different processes into precise analogies between these processes at different levels of complexity will clarify the underlying common process. This mapping involves making explicit the information feedback between levels. The mappings themselves will give insight into the processes and structures at each level. These mappings are again an ambitious task, and requires the deep understanding of the each level of complexity. On the other hand, there is a great deal of knowledge accumulated at each level of complexity by the respective sciences and vast amount of work has been performed in the sciences that straddle the levels of complexity, such as molecular physics, biochemistry, and ethnology.
Hand-in-hand with the process description is the structural description. One approach to devise a structural description, and the approach taken here, is to first catalog the major organizational entities of each level and the current major species, and if possible provide the history of evolution of species at each level. Analogous to the drive to catalog "life" by Linnaeus, this catalog can serve as lingua franca to generalize and unify the disparate phenomena that occur in the different fields of science. The problem has been that little attention has been paid to the various unified functional relationships of these structural components. In cataloging these structural, "material" phenenoma we will use functional names as well as their normal structural names.
Table 1 serves a sample of the top level listing of the major levels of complexity with example major species in that level complexity. Just as there is no perfect classification scheme in biology, there will not be a perfect classification in the science of complexity. On the other hand, just as wrong classifications served as a counterpoint foundation for discovery of better explanations as in the work of Lamarck, Cuvier, and Darwin in biology, so can this catalog and others serve as a framework of scientific inquiry for the science of complexity.
| Material
Complexity Level |
Abs-Species
Complexity |
Major Abs-Species | MacroSystem Lineage |
| 0 | Quanta (quarks, leptons) | Bosons, Neutrinos, Electrons | Universe |
| 1 | Particles (mesons, baryons) | Gamma rays, Neutrons, Protons | Galaxy System(Milky Way) |
| 2 | Atoms ( nuclei, plasma) | Helium, Carbon, Iron | Star System(Super Giant) |
| 3 | Molecules (monomers, polymers) | Solids (Si2O) Liquids(H2O), Polymers (Carbonhydrates, Nucleic Acids) | Planetary System(Earth) |
| 4 | Cells (prokaryotes, proctistia) | Thermophilics, Cyanobacteria, Proctistia | Biological System(Earth) - Gaia |
| 5 | Organisms (multi-cellular eukaryotes) | Fungi, Plantae, Animalia | Organism System(Gaia) - Hypersea |
| 6 | Families (genetic groups) | Social animals, Eusocial Invertebrates, Mankind | Family System(Hypersea) - Hyperland |
| 7 | Societies | Tribes, Governments, Corporations | Societal System(Hyperland) - Metaman |
| 8 | CyberSocieties | World Wide Web (internet mankind industry) | CyberSocietal System(Metaman) HyperMetaman |
Part of the problem with using the concept of complexity is the problem of defining exactly what consists of "the system" or the entity which encompasses the complexity. We will argue that some delineation's of systems are more natural than others for understanding how the complex things arise, such as living organisms. We will use the word complexity with a different meaning than the above usage's. We will use a particular meaning the word that include both process and structural aspects of the world. In other words, we are considering long-term, dynamic material complexity. Another way to view complexity, in a pure functional way is Robert Rosen's definition of complexity. His definition serves as long-term, static functional complexity. The correspondance between the two complexities is complex and is a future goal of Relational Science.
Regarding material complexity, if we look at nature and notice the entities that have been discover as building blocks in this complex world, we quickly find the results of science have given several levels of entity description. Through scientific consensus the words quanta, particle, atom, molecule, cell, organism, family, and society represent classes of entities that appear identifiable in some of the scientific disciplines. These words as concepts are useful in terms of a very naive definition of the word complex. If we take the simple usage of something is complex if "it is made of parts", then we find that a society is composed of families, a family is composed of organisms, an organism is composed of cells, cells are composed of molecules, molecules are composed of atoms, atoms are composed of particles, and particles are composed of quanta(bosons, leptons, quarks). This usage will serve as the basis of our notion of material complexity. It should be noted that in regard to functional complexity, the parallel concept is something is complex if "it is made of components", which is fundamentally different because concepts of "part" and "component" are different.
This notion of material complexity at first glance seems correct in
the intuitive aspect of common usage of word "complexity" and gives a nice
ranking of complexity that seems natural. That is, for example, societies
are more complex than molecules because societies at some level are composed
of molecules. Richard Dawkins in The Blind Watchmaker [8]
uses
this notion of complexity to discuss the evolution of life. But, this simple
usage of the word complex does not have a precise definition of "parts,"
and there is the problem of defining the extent of the whole. This naive
notion of complexity, although intuitively correct, must also address what
is relationship of the parts to the whole. And just as important, there
remains the question of what is the definition of the whole. Part of understanding
this part/whole relationship comes from examining the underlying process
of increasing material complexity. This underlying basic process is hypothesized
in the following section.
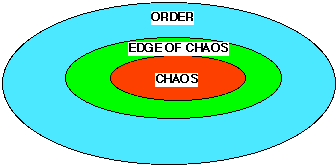
We aim to illustrate that this characterization of these three regimes appears to be the underlying process structure of the increasing material complexity of existence. Abstractly, each level of complexity has three basic regions as depicted in Figure 2a: the chaotic region, the order region, and the edge between the chaotic and order region. Figure 2b depicts the major level of complexity 2 in terms of these three regions. The chaotic region of a level of complexity supplies the evolutionary energy for the growth of an "edge of chaos" for the next level of complexity. The order region is the "material" area for storage of dynamic structures that were created by the process at the edge of chaos. The order region largely preserves the information at a level of complexity in these dynamic structures. But in addition, these structures in the order region can be fedback into the edge of chaos by energy fluctuations created by the turbulence of the chaotic region into the dynamic structures of the order region. Another simple metaphor to visualize the level of complexity, is view each level centered on a conceptual form of equilibrium in time and space, even though there is no such thing as an equilibrium in reality. The massive equilibrium, which is not exactly in equilibrium replicates and dissipates from that time and space center.
 -
-
A Level of Material Complexity Major Material Complexity Level 2
Figure 2a Figure 2bIn this paper, the discussion of levels of complexity will primarily center on major levels of material complexity. There are multiple levels of complexity between major levels of complexity, but characterization of these levels is difficult to define because the evolutionary nature of the edge-of-chaos process.
Microsystems are the dynamic structures that are combined to form more complex structures within macrosystems. Microsystems are the natural occurring building blocks that compose things: quanta, particles, atoms, molecules, cells, organisms, families, and societies. Microsystems are composed of several levels of underlying microsystems. A microsystem at major level N must have some forms of microsystems that are level N-1.
On the other hand, macrosystems form the context for microsystems. The
universe, galaxies, star systems, planetary systems, and the earth's biosphere
are examples of macrosystems. Macrosystems are dissipative/replicative
structures embedded in the universe. Macrosystems are formed from
the underlying process of chaos and order from within a larger context
that has direct lineage to the involution of the universe. All microsystems
and macrosystems are contained within at least one macrosystem context,
that is, the universe.
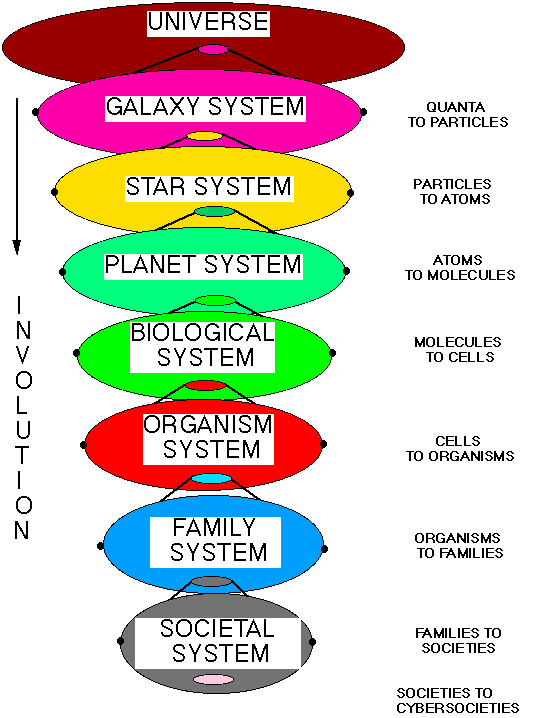
Figure 3. Involution of Our Existence: The Current Major Material Levels of Complexity
Figure 3 represents the current involution path of our existence, with the successive higher level macrosystems being a smaller and smaller part of the larger context in space, time, energy, and matter.
Both macrosystems and microsystems are examples of material systems. Material systems exist and the issue of their function is unspecified except having a function of existence. In the process of involution, material systems also have more functional roles, but the characterization of functional systems is different and there is no one-to-one correspondance with functional systems with material systems. In general the second function that material serve is as primarily dissipators or primarily replicators depending on its stage its life. Further analysis is necessary to characterize what kinds of dissipators or replicators there are, which in essence will be a mixture of dissipation and replication. The corresponding major functional systems to macrosystems are xemespheres, and corresponding functional systems of microsystems are xemes.
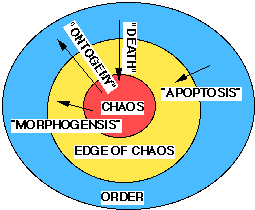
Another view of a level of material complexity is the characterization of the phases of dynamic organization of microsystems. Figure 4a represents a phase space of a level of material complexity. Figure 4b represents the major level of material complexity 2. The morphogenesis of simpler entities into a dynamic structure represent the phase change from chaos to order. For the complexity level 2, the morphogenesis is from particles to atomic nuclei. The growth from nuclear ion to atom by capturing electrons represents the phase change from the edge of chaos to order. The concepts of "death," "ontogeny," "morphogenesis," "apoptosis" are suitably generalize to include non-life phenomena.
 -
-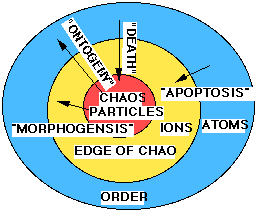
Figure 4(a) Figure 4(b)
A major level of material complexity phase space Major Complexity Level 2 Phase SpaceTo more concretely describe the process, we will use the example of the solar system as a major level of complexity 2. From a scientific point of view, this level of complexity is the probably the most understood level. On the other hand, ultimately, to fully understand a level of complexity, all the lower levels must be described also. However, to simplify the explanation of the process, the formation of hadrons and fermions in the complexity levels below level 2 will not be described.
In the solar system (complexity 2), the chaotic regime's center is at the center of the sun. The center of the sun is the most chaotic because of its temperature (15,000,000 degrees) and is reflected by the energy of elementary particles in the center. The entire sun is chaotic relative to anything more complex than nuclei of atoms, i.e., ions. The center of the sun is chaotic relative to individual atoms. In this chaotic region, no stable structure that consists of anything more complex can exist. That is, any matter of higher complexity that is drawn into the sun is subject to the destruction in terms of molecular structure and anything more, such as crystalline or cellular structure.
The order region (complexity 2) of the solar system encompasses the interstellar space affected by gravitation of the mass of the sun. This order regime surrounds the chaotic region centered in the sun. The order region (complexity 2) contains atoms wherever particular regions of mass that are not part of the sun and small enough and far enough away from the center of the sun to cool below nuclear reaction temperatures.
Any matter that is not frozen in the order region is between the order and chaos regimes. Thus, the geological active planets are on the edge of chaos of the solar system. Nevertheless, some frozen material in the order region such as comets and asteroids can be eventually pulled back into the edge of chaos by virtue of their long-term trajectories and interaction with the established planets. In fact, the planets were formed by an aggregation process, where the largest planetesimals formed by gravitational and electromagnetic waves of entire stellar mass served as centers on the edge of chaos (material complexity 2) of the solar system.
The next major level of material complexity
The edge of chaos at one major level of material complexity contains the chaotic region for the next higher level of material complexity. A molten center of a planet is on the edge of chaos of solar system (material complexity 2) which serves as the atomic chaotic center (material complexity 3) to form molecular compounds. Figure 5 represents the phase space of major level of material complexity 3.
Figure 5. Major Material Complexity Level 3 Phase Space
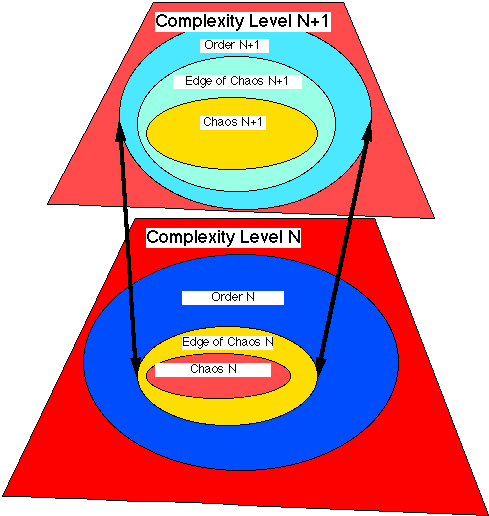
Figure 6. Two levels of Major Material Complexity.
Figure 6 illustrates the arising of the next level of material complexity from the level below. The edge of chaos region N-1 contains the chaotic region N. The illustration is conceptual, because the next higher level of material complexity is physically contained in the lower level of material complexity. Moreover, the region between order and chaos, "the edge of chaos," is a not physically continuous region, and the edge of chaos is very small compared to the order and chaotic regions. ("The edge of chaos" is probably approximately 10-7 smaller in mass-energy than the chaos region, and approximately 10-7 smaller in space-time than the order-region.)
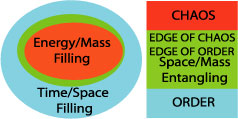
Figure 7. Information Filling of the three material phases of existence
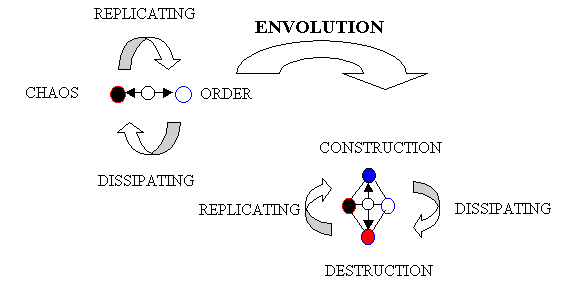
It is posited that in reality (e.g., our universe), replication and dissipation cannot be separated: one implies the other. Replication is dissipation of order, and dissipation is replication of disorder (chaos). In the Hegelian tradition, order implies disorder and disorder implies order. Replication and dissipation are entangled in any part of existence.
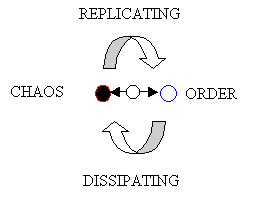
Figure 8. The Replication/Dissipation Metaphor
In reality, replication and dissipation are entangled, for there is no such thing as pure replication or pure dissipation. Any form of replication implies a form of dissipation and visa versa. What is major difference between replication and dissipation in the non-pure abstract? Given that replication is dissipation of order, and dissipation is replication of disorder, what does this imply? Given that any "order" must be instantiated in terms of a "measure", this implies that at least one "dimension" exists. At a minimum, replication must dissipate order along one dimension in some degree. What does "dissipate along one dimension in some degree” mean. Essentially this is a construction of the dimension into a configuration. Obviously many kinds of replication may involve dissipation of order along several dimensions or the beefing up of a dimension. Given dissipation is the opposite of replication, then it stands to reason that dissipation must replicate disorder in at least one dimension in some degree. What does "replicate disorder in at least one dimension" mean? Essentially this means a destruction of a dimension into a configuration. Obviously many kinds of dissipation may involve replication of disorder along several dimensions or partial diminution of one. Therefore in the abstract, the relationship between replication and dissipation is relation between construction and destruction of dimensions into a different configuration. The creation and destruction of dimensions must involve entanglement between dimensions, and the first set of "dimensions" that mediate other "dimensions" must include a notion of "time" (time0) which is "pure dissipation" and "space" (space0) which "pure replication". The time0 "dimension" is not a conventional dimension in that it isn't reversible, since it must be "pure dissipative" (unreal). Likewise space0 "dimension" is not a conventional dimension in that it acts like "pure replication" an infinite set of dimensions, not being specific in the any "dimension". There are few simple models that mimic some of the behavior of these dimensions: names of these models include "zero," "infinity," "negative infinity."
The description of Dissipative/Replicative processes is in the context of a global Dissipative/Replicative structure (the so-called multiverse), but at the most primitive level, one cannot talk about what it is constituted of. One must posit almost complete randomness and almost complete order as the context, but the form must have the property of dissipation and replication.
Darwin’s evolutionary metaphor is an essentially a near-equilibrium model. It is simpler than the above metaphor and uses the word reproduction rather than replication and it does not emphasize the words metabolism or “natural selection” as a form of dissipation. Lastly, “mutations” just happen. One might model the general Darwinian metaphor as the following.
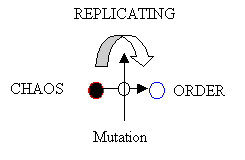
Figure 9. A Model of Darwinian Evolution
There are other uses of the word “evolution.” The most common use of the word evolution refers to Darwin’s model of how life changes. Darwinian evolution, which assumes “reproduction” and “metabolism” and typically is only discussed in terms of the multicellular organism part of life, is a particular model of how things change. On the other hand, the word evolution is also used when refering to changes in the universe, such as the birth and death of stars and the changing of galaxies. Higher forms of “evolution,” that is, when talking about human social change, there is a reluctance to view it in a “Darwinian” light because of the political overtones. Lastly, “evolution” in any context is rather ambiguous, because it sometimes is meant to include “progress” or in other cases, is meant to be devoid of “progress.”
The word “devolution” although not used extensively in science captures the essence of “decay,” in a vague evolutionary sense. In reality, equilibrium, is in some sense, is another way of viewing “decay” or “devolution,” or in Prigogine’s words, a kind of death. The ultimate “death” is going back into randomness, where complete randomness is the “real” death. With levels of complexity, a death is just reorganization down to an underlying material complexity.
The other major scientific metaphor, in some sense opposite of evolution, is the second law of thermodynamics. It is asserted that it governs all of matter; however, this metaphor assumes an “isolated” or “closed” system, which cannot be the case with the universe – the universe is not in equilibrium. In fact, pure equilibrium does not exist – all “equilibriums” must be dynamic, or in some metaphoric sense, living. Clausius’s metaphor is in reality a model of death and decay. A simplified model of entropy is the following:
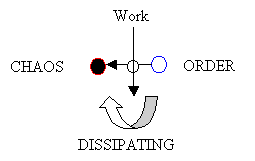
Figure 10. A Model of Clausius’s Entropy
Syntactically there is very little difference between the two metaphors, entropy and evolution – they are simple models, to a degree mirror images of each other. So a more complete metaphor would be to combine the two models of Clausius and Darwin to form a replicative/dissipative structure.
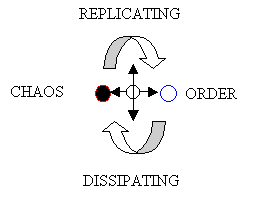
Figure 11: Unification of Darwin’s and Clausius’s Metaphors
This model can be applied to itself, thus creating multiple levels of complexity – roughly, there can be an evolution of complexity.
Hence, I will use the two words: involution and envolution, as semi-neologisms, to refer to the “evolution of complexity” but in the wider context of both life and non-life including the changing of: bosons and the universe, to eucaryotic multicellular life and Gaia, to cyberentities and the Web. “Involution” is the evolution of material (structure) complexity. “Envolution” is the evolution of functional complexity. Both involution and envolution are entangled, for if there is no structure, then there is no function, but also if there is no function, then there is no structure.
The relationship between dissipation and replication is examined from both a functional complexity and material complexity point of view. A “replicative/dissipative” structure is the material metaphor for naming the entity involved in the complexity, but recognizing the fact there is always a context that surrounds the entity. There is a discrete continuum from non-life to life in the “involution” and “envolution” of existence.
Figure 12. Two-levels of Functional Complexity: Envolution
Returning to our material example of complexity level 2, in the initial formation of the sun, the matter not part of the hot, gaseous sun is on an edge of chaos(complexity 2). As the mass in the vicinity of formation of the sun collapses into a stable star, the matter farthest from the chaotic center crystallizes into frozen planets and asteroids. The frozen matter becomes part of the order region. Any atomic nuclei in the order region attract electrons to form atoms and then combine at the molecular-level (complexity 3) based on the geology of the physical mass in the area. Faster the cooling to solidification and crystallization, the fewer species of molecular chemicals have chance to form. If the dominant local population is of a gaseous nature at the temperature, then the nature will be of "chaotic order", that is, gas at near-equilibrium. If the dominant local population is of a solid nature at the temperament, then the nature will be "ordered chaos" reflecting the fact that atoms never stop moving, even in solids.
Figure 4b represents a type of phase space of the matter at the level of major material complexity 2. Individual entities go through a morphogenesis process. At the solar system of complexity, material complexity level 2, the aggregation process is a morphogenesis process that combines protons to create helium nuclei. Besides being the center of the creation of light nuclei, the sun has collected nuclei that were created from previous generation stars. These nuclei came from the order region of the galaxy (complexity 1). The heavy atoms of previous generations were stripped of any molecular structure by the high energy in the chaotic region of the sun. Sometime during and after the sun formation, the many of planets were formed consisting almost exclusively from these previous generated nuclei. As the planets formed, the many of nuclei in the planets and asteroids quickly matured and stabilized to atoms by acquiring the electrons because temperatures were below plasma temperatures.
All the planets that continue to cool but have not become geologically dead are still on a edge of chaos (material complexity 2). In the formation of planets, the large planetesimals that served as the collection point of the planet define this edge of chaos (material complexity 2). Once a planet has cooled sufficiently, there is the possibility of ions acquiring enough electrons to form atoms or combining with other ions to form molecular compounds. In the beginning the combinations would be simple. However, as the planet continued to be chaotic in movement of atoms(material complexity 3), the forming and destroying of molecular compounds would continue to take place. It should be noted that even in "frozen" asteriods, there is to some degree exchange of electrons and ions or cations (most notably on the surface), atoms and molecules are dynamic to a degree forgotten by normal abstraction.
In the gas giants, gravitation can retain the dominant atomic species of hydrogen and helium, thus the dominant molecular species would be hydrogen and helium molecules. In the smallest planets or moons, the geologic processes will continue for some time after formation, but lose most of the light gases into interplanetary space. These smaller bodies are left with the heavier elements dominating the geologic processes.
The next level of major complexity above the star system (material complexity 2) is the planetary system (material complexity 3). With geologic processes continuing on the planets, the creation of more complex molecules would proceed. Each planet is a center of atomic chaos (material complexity 3), that is because of the heat from radioactivity and pressure, no molecular bonds can be maintained. The planet surface and the interplanetary space is the order region (material complexity 3). The chaos, edge of chaos, order regions of complexity 3 are contained in the edge of chaos (material complexity 2). Typically, a edge of chaos of complexity 3 is the planet's surface. In the case the gas giants, their geologically active moons are also on an edge of chaos (material complexity 2). If there is no interaction between the spatially separately atomic chaotic centers, then there are separate region of edge of chaos (material complexity 2) for each atomic chaotic center (material complexity 3).
The earth provides a stable source of atomic chaos because of its size, having a singular moon, and its distance to the sun. The earth appears to be the closest planet to the middle of the edge of chaos of the solar system. The earth's surface is the center for the moderately complex elements of carbon, oxygen, etc. The earth is the only example that humans can observe at present that sustains higher, major levels of material complexity than three.
There remains a great deal of work to detail all the major levels of complexity and start classifying levels of complexity between the major levels. There is a great need to begin the field of comparative complexity, which can help in understanding our world better.
An entity X is complex if it has "observable" parts P(i) that can "observed" as entities outside the entity X. To "observe" P(i) outside of X, P(i) must be able to "operate" and maintain its internal organization in the manner it did inside of X until the "observation."
Word Usage: Major Material Complexity
The property of being material complex. An entity X has major material complexity of one more than the maximum of the major complexity of its material parts. A entity X is more complex than another entity Y if all the parts in Y exist in X and there exists a part P(i) in X that cannot exist in Y as a part of Y without destroying fundamental organization of the entity Y and the part P(i).
Word Usage: Fundamental organization of material
A structure with material parts: where relationship of the parts are defined in terms of a ongoing process that requires all of the essential parts of an entity. Without the process continuing, the all parts in the structure will no longer maintain their same physical interaction with the other parts.
Example 1: A molecule is more complex than an atom. E.g., a there exists a part P(i) (the oxygen atom) in a molecule X (carbon dioxide) that cannot exist in the atom Y (silicon). In other words, one cannot take the oxygen from a molecule of carbon dioxide and put it in the atom silicon and keep an atom oxygen without destroying the identity of the silicon atom and the oxygen atom. Atomic fusion of silicon and oxygen destroys the fundamental organization of the entity, the silicon atom, and the oxygen part of the molecule carbon dioxide. Combination of the atom silicon and the oxygen part of the molecule carbon dioxide can occur to form silicon oxide; however, this is a molecule and the oxygen part is not a part of the atom silicon.
Example 2: A organism is more complex than an cell.. E.g., a there exists a part P(i), the human cell, in a human organism X that cannot exist in the cell Y (bacteria). In other words, one cannot take a cell from a human organism and put it in the cell bacteria and keep the human cell without destroying the identities of the bacteria cell and the human cell. Cell fusion of between bacteria and human cell destroys the fundamental organization of the entities: the bacteria cell and the cell of part the human organism. Combination of the bacteria and the human cell of the can occur, such as E. coli in the human gut. Nevertheless, this combination is a part of a organism and the human cell part is not a part of the cell bacteria.
Stock, Gregory, MetaMan, Simon and Schuster, 1993
McMenamin, M. and D. McMenamin, Hypersea:
Life on Land, Columbia University Press, 1994.
[1] Cohen, J., and I. Stewart, The Collapse of
Chaos, Penguin Books, 1994
[2] Prigogine, I. and I. Stengers, Order out of Chaos, Bantam Books, 1984.
[3] Kauffman, S. The Origins of Order, Oxford University Press, 1993.
[4] Gell-Mann, M., The Quark and the Jaguar, WH Freeman, 1994.
[5] Wolpert, D., The relationship between Occam's Razor and Convergent Guessing, Complex Systems, pp 319-368, Vol 4, 1990.
[6] Bennett, C.H., In Emerging Syntheses in Science, D. Pines, Ed. 1988.
[7] Lloyd, S. and H. Pagels, "Complexity as thermodynamic depth, " Annals of Physics, pp 186-213, 1988.
[8] Dawkins, R., The Blind Watchmaker, Norton & Company, 1987.
[9] Langton, C., Computation at the Edge of Chaos, Phase Transitions and Emergent Computation, Physica D, pp12-37, Vol 4, 1990.
[10] Mitchell, M., J. Crutchfield, and D.
Hraber, "Dynamics, Computation, and the Edge of Chaos: A Re-Examination,
G. Cowan, D. Pines, and D. Melzner (editors), Integrative Themes, Santa
Fe Institute Studies in the Sciences of Complexity, Proceedings Volume
19. Reading, MA