

     |
Loading
|
The Edge of Chaos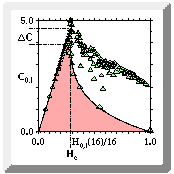 Chris Langton when
playing with self-reproducing cellular automata with threshold of added
noise, discovered a regime at particular theshold value, where there is
a transition between where the state of the automata eventually repeats
itself and state where there is completely random generated states that
never repeat. Coined by Doyne Farmer as the "edge of chaos" this
regime is between the chaotic regime and the order regime.
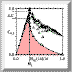
Jim Crutchfield has mathematically analyzed this transition and determined
that there is a peak at the "edge of chaos" where there is a maximum
of information. The edge-of-chaos is where COMPLEXITY
resides Chris Langton when
playing with self-reproducing cellular automata with threshold of added
noise, discovered a regime at particular theshold value, where there is
a transition between where the state of the automata eventually repeats
itself and state where there is completely random generated states that
never repeat. Coined by Doyne Farmer as the "edge of chaos" this
regime is between the chaotic regime and the order regime.
Jim Crutchfield has mathematically analyzed this transition and determined
that there is a peak at the "edge of chaos" where there is a maximum
of information. The edge-of-chaos is where COMPLEXITY
resides
In actual fact, the metaphor in form of the phrase "edge of chaos" is misleading, for this "edge" is more like a dynamic discontinuous surface or volume depending on the complexity of the cellular automata. Moreover, the edge-of-chaos is also the "edge of order", depending on which side (chaos or order) you are looking from. One can visualize this metaphor as a phase space and model natural systems
in this way.
Figure 1. A Macrosystem: A Level of Major Material Complexity In natural systems, the actual size of the edge-of-chaos region is very small compared to chaotic and ordered regimes (approximately 107 smaller in mass-energy compared to the chaotic region and 107 smaller in space-time compared to ordered region). The chaotic region has most of the mass and energy, but the ordered region occupies most of the space and time. The chaotic region supplies the evolutionary energy for the growth of the edge-of-chaos. The order region is the ``material'' area for the storage of dynamic structures (i.e., microsystems). If the edge-of-chaos is big enough, then you can have multiple levels of material complexity. On the earth the atomic chaos of the center of the earth is next to
the molecular chaos of the surface of the planet, which is the edge-of-chaos
when compared to the ordered regioned of the atmosphere.
|