Yet faith in false precision seems to us to be one of the many imperfections our species is cursed with. -- Dylan Grice
Quantum mechanics, with its leap into statistics, has been a mere palliative for our ignorance -- Rene Thom
Give me a fruitful error any time, full of seeds, bursting with its own corrections. You can keep your sterile truth for yourself.
Vilfredo Pareto
There are two ways to do great mathematics.
The first is to be smarter than everybody else.
The second way is to be stupider than everybody else—but persistent.
Raoul Bott
(under construction)
Formatics: Precise Qualitative and Quantitative Comparison. Precise Analogy and Precise Metaphor: how does one do that, and what does one mean by these two phrases? This is an essay, in the form of an ebook, on the nature of reality, measure, modeling, reference, and reasoning in an effort to move towards the development of Comparative Science and Relational Complexity. In some sense, this ebook explores the involution and envolution of ideas, particularly focusing on mathematics and reality as two "opposing" and "fixed points" in that "very" abstract space. As Robert Rosen has implied there has been (and still is going on) a war in Science. Essentially you can view that war as a battle between the "formalists" and the "informalists" -- but make no mistake the participants of this war are united against "nature" -- both are interested in understanding the world and sometimes predicting what can and will happen, whether that be real or imagined. So... I will ask the questions, for example, of "what could one mean" precisely by the words: "in," "out," "large," and "small." The problem is both Science and Mathematics are imprecise -- but this sentence contains fighting words and is impredicative, to say the least. In my father's terms, it is important to distinguish between order and organization, and understand the difference. Lastly, for now, the concepts and their relations, in the circle of ideas of "dimensions of time" and dimensions of energy along with the dimensions of space and dimensions of mass will be explicated, as I evolve (involute and envolute) this ebook. SO WHAT IS HE TALKING ABOUT? Let me try to explain.
Table of Contents
Prolog
Praeludium
Preface: Breaking the Spell of Mathematics
Chapter I -- Introduction: It's What Mathematicians Do
A Brief Look at Octonions
Opening a Can of Worms
Destruction of The Code
Chapter II -- Constructing the Code: The Problem of Modeling
Science, Math, and Modeling
Initial Look at the History of Science
One Problem with Modeling
A Brief Look at Complicating
A Problem with Mathematical Words: Number, Dimension, and Space
Modeling and Formal Systems
The Nature of Entailment
Natural Systems and Formal Systems
Relational Complexity
Chapter III -- Breaking the Code: The Nature of Form
Losing and Gaining
The Dimension of Dimensions
Chapter IV -- Proving the Code: Encoding and Decoding
Slapdown, Insight, Inference
Slapdown
Insight
Inference
Chapter V -- Creating the Code: On the Nature of Abstraction
Chapter VI -- Transforming the Code: On the Evolution of Ideas
Making the best of it: Planck
Brilliant Mistake: Kepler
Same but Different: Born versus Schödinger
Chapter VII -- Fabricating the Code: Numbers, Symbols, and Words
Chapter VIII -- The Code Game: Mathematics and Logic of Replication and Dissipation: Analysis, Synthesis, Abstraction, and Comparing
Cakes and Frosting
Chapter IX -- Architecting the Code and Meaning: Relational Science, Formatics
Time Sheets
Chapter X -- Conclusion: On the Structure and Process of Existence
Science is my religion
Christiaan Huygens
Ideas do not have to be correct in order to be good;
its only necessary that, when they do fail and succeed (and they will),
they do so in an interesting way.
Robert Rosen hacked by David Keirsey
I like any used idea that I encounter ... except, except ... the ones that cannot be understood.
Never accept an idea
as long as you yourself are not satisfied with its consistency and the logical structure
on which the concepts are based.
Study the masters.
These are the people who have made significant contributions to the subject.
Lesser authorities cleverly bypass the difficult points.
Satyendranth Bose
Hindsight is the best sight.

This garden universe vibrates complete,
Some, we get a sound so sweet.
Vibrations, reach on up to become light,
And then through gamma, out of sight.
Between the eyes and ears there lie,
The sounds of color and the light of a sigh.
And to hear the sun, what a thing to believe,
But it's all around if we could but perceive.
To know ultra-violet, infra-red, and x-rays,
Beauty to find in so many ways.
Two notes of the chord, that's our poor scope,
And to reach the chord is our life's hope.
And to name the chord is important to some,
So they give it a word, and the word is OM.
The Word, Graeme Edge
In Search of the Lost Chord
"There is geometry in the humming of the strings,
there is music in the spacing of the spheres."
-- Pythagoras
in-form == 1
ex-form == 0
form == -1
Now Moufang it and Emmy ring it two. Make Lise Bind. Oh, Dedekind bother, it's a unReal hard cut.
But,
Never mind, Hilbert doesn't bother. Such a Dehn mine-d vater.MJ Golay to the Ri-emann'-s-kew, the R. Hamilton and Hamming to rearrange and recode, the 4th Prime Milnor Poincaré to re-solder.
Hatter would be mad. From Lagrange, W. Hamiliton, Erwin to Lindblad.
Abandon the Simple Shannon.

Two notes of the chord, that's our poor scope,
And to reach the chord is our life's hope.
And to name the chord is important to some,
So they give it a word, and the word is:
Di-vision

To Subquotient, or Not Subquotient,
That is the question!The divisor status, of the lattice, oh my, Times, Rudvalis.
Crack the Dirac, Landau beseech the damp Leech.
It's a Monster Conway Mesh, Mathieu's Stretch, Jacques' Mess, Janko's Sprains, and Einstein's Strain.
Never mind the mock theta, Ramanujan's gap, Namagiri dreams.No Tegmark or Linde, but Verlinde in name. It's all but Feynman's streams,
and weigh.
Such a Prime rank, any such Milnor's exotic sank.
No mess, no Stress, but Strain. Tensors Bohm and bain.It's Held together. Dr. Keirsey is here to re-frame.
It Works! Much to lose and A Gain.It's Life Itself, More AND Less, a game.
Mathematics is a game played according to certain simple rules with meaningless marks on paper.
David Hilbert
There's no sense in being precise when you don't even know what you're talking about.
John Von Neumann
Formal axiomatic systems are very powerful.
Kurt Gödel
Do not worry about your difficulties in Mathematics. I can assure you mine are still greater.
Albert Einstein
What is the relation between language, the engine of human communication and inferential entailment, the engine of mathematics and logic? Even though my father's mathematical knowledge was strong in statistics and rather limited or lacking in other areas, such as advanced algebra or calculus, he had reservations on what I implied mathematicians have been saying. Being vaguely aware of Cantor's boo-boo, he maintained that the phrase [ a "set" is a "subset" of itself], didn't make sense. Being youthful and ignorant of most things but exposed to “new math” my hubris knew no bound -- I would teach my father. I quickly learned, yes, he was right in some degree. I announced [a set is not a proper subset of itself]. Nevertheless, I maintained the statement that a set can a subset of itself could make sense in a certain context, if you defined it that way. This did not placate him. He suggested that I (and maybe "mathematicians") were abusing the word “set,” and there was no such thing as a subset. Our debate centered around the questions of what words meant, the nature of language, and an underlying issue of "self-reference." He would not defer to me and my newly acquired language, mathematics, and my youthful mathematical knowledge. I eventually understood his real objection several decades later, which he never fully understood, and we had debated many things in a similar vein for a half of century. My study and development of Comparative Science, in the form of Relational Complexity, the problem of impredicativity (which relates to "self-reference") and confusion of many kinds and degrees of conceptual infinities, zeros, and unities (e.g. 1) in trying to model things attest to this fact.
Being a “hard” science kind of guy by nature but always being questioned by my “Gestalt” psychologist father, I always, in the back of my mind, questioned the basic assumptions taught to me in school -- like the physics concept of “mass.” I couldn't put my finger on exactly what was wrong or what issues were being finessed, for I figured that I was either ignorant or not bright enough to know better. As I went through school I vaguely noticed the reductionistic methods of conventional science and mathematics, although I embraced and believed in these methods as sufficient most of my life. I had started examining the world critically very early, ever since my mother started reading to me "The World We Live In."; I have been reading about the natural world ever since. In college, I started as a Chemistry major including a course in Thermodynamics, but took Electrical Engineering courses until I abandoned EE (and Stokes theorem) for an easier subject (for me), and a new school, The School of Information and Computer Science, UCIrvine -- for I knew Computers very well, for I was skilled in using a Sorting Machine and assembly language. Information ("bits") were in my blood and finger tips. (Yes, alas I am five years older than Bill Gates and Bill Joy, and my interest was never in business, ala Malcolm Gladwell's Outliers ).
As a young researcher, armed with my experience of things "digital," I also began to be enamored with my own vision of the universe, a similar vision of Laplace's clockwork universe or Ed Fredkin's and Steve Wolfram's vision of the universe as one big cellular automata. I grew to love all of conventional science, computer science, and mathematics. I still do. But I finally pinpointed the “flaw” when I discovered Robert Rosen's rigorous explanation of what “really” my father had tried to tell me. Unfortunately, and naturally, my father did not realize in detail what Rosen is saying: the form of entailment is limited in conventional science and mathematics. Rosen demonstrated the limitations in biology and hinted at other limitations, physics in particular, but his reasoning and arguments are applicable to all of science, computer science and mathematics. Demonstrating this applicability is part of what this book is about, but I will try to go beyond to suggest and fabricate notation, words, and precise methods for reasoning, observing, and comparing: in the form what might be called Relational Science. My father's take on science and mathematics was a more of a global view: conventional science, mathematics, and computer science often gets confused and impressed by its own words or formalisms. Not clearly understanding your key (or "hammer") words or formalisms, in other words, not knowing their strengths and weaknesses, will get you in trouble.
Having a running debate on what words meant, had made my father and myself explore the nature of things to a depth and in a way not conventional. We eventually turned to the question of What is Mathematics? -- each of us having our own, differing view.
Growing up, as part of work study, I learned early about programming and computers(essentially a form of discrete mathematics). I saw and used first generation computers (using vacuum tubes) in high school (starting in 1965). I independently encountered Cybernetics, by Norbert Wiener, in high school and devoured Ross Ashby's Introduction to Cybernetics so my mathematical education was less than ordinary. It had struck me singularly Wiener's statement that Information was negative entropy. That statement has haunted me, all my life. What does that statement imply?
And of course, being early in the field of programming, I learned a few "languages," to name a few, Autocoder, FORTRAN, COBOL, PL/I, 360 Assembler, machine code, MACRO-10, Algol, APL, TRAC(a reduction language), L3 (thanks John), etcertera etcertera etcertera, and, ah yes, LISP --- after awhile frankly you name it, I'd learn on the fly. I learned about how the early computers were designed and built (including the underlying physics), and how a diversity of computer languages were constructed and used and eventually died. Eventually my education included all areas of computer science, including a very strict and conventional course in Mathematical Logic, taught by a professor who was a "grandson" (PhD) of Church. Forced by necessity to learn it so I could teach it, I became very familar with theories of computation. My Computer Science expertise became more detailed; eventually I wrote an Artificial Intelligence PhD thesis about how one might make a computer program that could learn new words. In wrestling with "what words mean" to a computer, in conjunction with studying "what symbols mean" to a computer, I gained insight.
That research on learning new words was partly motivated by my experience in living in Japan for a brief time, not having known the Japanese language at all, when arriving there. Being an young adult (24) I watched myself learn language (formally and informally) and took a stranger in a strange land view of my interactions with individuals. Teaching English and learning Japanese simultaneously, I couldn't always use my native language to communicate with a very different culture than my own. This included a Thai lady who knew as much Japanese as I did, which was not much – basic communication between her and me, and her Japanese husband, the two who I was teaching English was definitely primitive. Moreover, when teaching English to Japanese adults, I was amazed by my ignorance of my own language. I could speak and write English, but I really didn't know, for example that we had six verb tenses (Japanese has one and a half) and why. Similar to Einstein's experience in learning about space and time, the result of this experience I examined the notion of “understanding” and “language” from a very questioning and analytic point of view -- looking at my language and culture, the Japanese language and culture, and other foreign languages I failed to learn (German and Spanish) in my previous schooling -- from a very childlike but sophisticated way. Recently in the last two decades, I have looked into mathematics, quantum mechanics, and other domains of discourse, such as, cosmology, biology, and history from that similar agnostic, naive, and sophisticated point of view.
After Japan and Graduate school, I had moved to professional research. I concentrated on natural language processing and mobile robotics, two forms of Artificial Intelligence, subfields of computer science. I tried to teach (or build) computers to understand language or to behave intelligently. Notably, I was part of a team who created the software for the first operation of an autonomous cross-country robotic vehicle. The Panglossian enthusiasm for robotics, I and others within the AI community projected into future and had similar visions, first evidenced by Hans Moravec's concept of "mind children," prestaging the web and the vague concept of the noosphere. All along I continued to take an interest in “reality” in the form of reading extensively in the areas of non-fiction, particularly in history(of mankind and the physical world), science, and mathematics. Being in the computer field from a very early age, I watched and participated in the beginning of the Internet (ARPAnet). I particularly remember the refrigerator-sized Honeywell's IMP (interface message processor) sitting in the computer center of UCSB in 1969. Having expertise in Hypercard and Emacs I started building my own "mind children" slowly recognizing hints of the emerging Hypermetaman. The start and development of the Web has been of particular interest and focus, I discovered WAIS, Gopher, and Mosaic very early in the birth of the Web. Lastly, I also acquired some specialized expertise in human nature, namely, some of my father's expertise in human personality, intelligence, and madness(psychopathology).
Because of my expertise in personality, I have been asked by many individuals in search of them"selves": “who they are.” More than often I tell them it's sometimes easier to understand who they are not. So in the same vein, to try to answer this question What is Mathematics?, I will ask questions, such as, “What Mathematics is not. ”
Starting as a Chemistry major, moving to Electrical Engineering, I had always greatly enjoyed and did well in school with mathematics until I encountered "fields of polynomials" in second year college mathematics (for engineers), where upon I couldn't "relate to it," or really understand it, and decided computers (before most knew anything about them) were my ticket. I moved to UCIrvine, Department of Information and Computer Science. I have revisited mathematics proper, about 30 years later, when I "could relate" to the accumulated mathematical jargon of 2000 years (number, space, rings, homotopies, etales) and started understanding the underlying ideas beyond the obscuring detail and abstract "words" sometimes in the guise of symbols. In studying theories of computation, mathematical foundations, and some of the latest in mathematics and physics one can be overwhelmed by the complexity(including forgetable details) and the abstractness. But, in particular, we will find that mathematics is not physics, just as much as physics is not mathematics, despite the fact they are often conflated implicitly. In some sense, I will be looking at the physics of mathematics and mathematics of physics to understand what there is in common and what the difference is.
Robert Rosen had questioned the current approach of science in its use of the Newton-Turing paradigm, which includes the diverse domains such as modern string theory and molecular biology. In reacquainting myself with the domain of biology and the possible origins of life, important questions raised by Lynn Margulis and James Lovelock renewed my interest in the relations between life and non-life. So beyond this one might find it useful to ask the questions of what is the life of mathematics and what is the mathematics of life.
It was a shock. It happened as I was reading Life Itself, by Robert Rosen. I remember it very vividly. I still can recall it mentally: the time and place. My neck hairs stood on end. It was a sudden realization -- an epiphany. It was like the coming from "nowhere" from "everywhere", the crystalization of order from the surrounding "invisible" chaos. I visualized it as an ideal empty Euclidean 3D sphere -- there it was. My view of science, and the world, changed in that instant. The emptyness (or "thinness") of recursive functions in regards to entailment. Positing reason as a given, an axiom, a faith -- was necessary -- a metamathematical religious tenant. So it is important to look at the what is the religion of mathematics and what is the mathematics of religion.
Lastly, it is important to examine the nature of reality, measure, reason, reference, and modeling. For physics, biology, economics, computer science, and the mathematics fields are not particularly introspective and informed about the human mind and its beliefs. The task is: doing reasoning, observing, and modeling -- which is what science is mostly about, and – going beyond computational (or conventional mathematical) models, however simple or complex -- to more abstract, partially semantic methods, but still precise inferencing. As Robert Rosen has said "when studying an organized material system, throw away the matter and keep the underlying organization." This also applies to mathematics. To put it baldly: "throw away the numbers and symbols, and keep the underlying organization and assigned meaning." Or as my father had said, ideas are always within a context and do not confuse the idea of organization with the idea of order.
To do this right, one must examine closely mathematics, physics, biology, computer science, and human action. And of course, one must know a lot of history -- and when I say history -- I mean ALL of history -- including, for example, the history of Moore machines, Clifford algebras, affine spaces, bosons, particles, atoms, molecules, procaryotes, eucaryotes, Hypersea, mankind, Metaman, and the Web. In this manner one will have a better technology to predict the future of humankind and its mind children.
GoodReads
LibraryThing
No one shall expel us from the paradise that Cantor has created for us.
David Hilbert
A scientist can hardly meet with anything more undesirable than to have the foundations give way just as the work is finished.
Gottlob Frege
No one means all he says, and yet very few say what all they mean for words are slippery and thought is viscous.
Henry Adams
Number theory is a special categorization
John Baez
Never mind, Hilbert doesn't bother, Such a Dehn mine-d vater
What is mathematics? There is a simple answer to this question – a flippant version is: “It's what mathematicians do.” This was my answer to my father when he asked me the question (rhetorically) and I was exasperated, exhausted by arguing with my father in our mismatch with our "words," -- mathematics in particular. However, this ebook will answer that question in a more complicated way. It is known that David Hilbert failed in his program, but since Kurt Gödel demolished that program, few have taken an overall look at the meaning or purpose of mathematics and logic to see what kind of picture that emerges from that deconstruction. I am interested in how mathematics "works" -- in some sense I am interested in how Mathematics is implemented as a language, whereas most just "use" it and are not interested on examining it in detail or systematically.
On the other hand, I am very well aware of the many efforts within and outside of mathematics looking at notions of complexity or theoretical characterizations of logic that have been applied to mathematics and logic before. For example, Kolmogorov and Chaitin complexity or Topos theory, model theory, domain theory, and paraconsistent logic are interesting and useful knowledge domains that can contribute to an examination of mathematics.
However, what is the point of mathematics?
Mathematics is a language.
Josiah Willard Gibbs
It's a language – and its primary function is to model – in particular its primary function has been to model science, or in other words, reality. Mathematicians find interest in determining the “reality” of mathematics, but mathematics that is “realizable” is probably closely related to what is physically realizable, which includes things beyond physics. This issue will become more important as time goes on. The crisis in Physics, with string theory having no experimental basis other than what has been discovered before (e.g., relativity) has lead to the question: is string theory, mathematics or physics? Mathematicians would say string theory is not mathematics rather it's physics, but where's their proof? All they can do is throw words at the problem -- those fuzzy meaning things -- those slippery things -- in the form of natural language, no different than lawyers and politicians or similar criminals. (Of course, they can ignore or be oblivious to the problem, like politicians.)
We can’t solve problems by using the same kind of thinking we used when we created them.
Albert Einstein
I quickly came to recognize that my instincts had been correct; that the mathematical universe had much of value to offer me, which could not be acquired in any other way. I saw that mathematical thought, though nominally garbed in syllogistic dress, was really about patterns; you had to learn to see the patterns through the garb. That was what they called “mathematical maturity”. I learned that it was from such patterns that the insights and theorems really sprang, and I learned to focus on the former rather than the latter. -- Robert Rosen
I will never listen to the experts again!
Richard Feynman
In theory, there is no difference between theory and practice. In practice there is.
Yogi Berra
Much of mathematics was developed by "non" mathematicians -- Archimedes, Newton, and Gauss are considered the giants of mathematics, significantly used the natural world to create their ideas in mathematics. It has been primarily "physics" and "engineering" that propelled mathematics in the last three centuries, but the methods that worked in the past usually don't work as effectively for harder and new problems of the future, such as -- what is the future "evolution" of humankind and the Web? The problem of addressing "function" (as opposed to structure) has not been done well in mathematics. The field of economics has tried to use conventional mathematics, and has generated many baroque "theories" of little use except creating academic empires or meteoretic financial groups (e.g. LTCM). Biology and evolution involve more dynamic and functional questions, and mathematics will need to go beyond structural ideas to progress significantly. No doubt the vast majority of mathematicians will not be interested, hence it might be better to not characterize the development as mathematics or metamathematics. Maybe a neo-logism is more appropriate: Formatics.
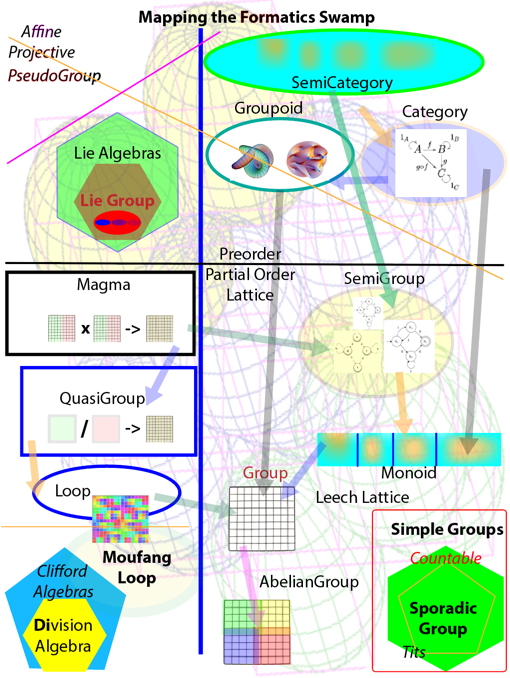
There are many measures and characterizations of complexity and power of expressiveness that have been applied to both to computation, logic, and mathematics, but most of the time those characterizations or measures have concentrated on the thing that mathematics and logic tries to represent, rather than trying to look very closely at the thing (mathematics and logic) that it can represent -- the thing -- reality. In other words, I am more interested in Mathematics Itself, not its canonical forms or its various instances of representations, whether that be Number theory, Topos theory in the form of Closed cartesian categories, Lie Algebras, Intuitionist's logic, Turing Machines, Model Theory, Inconsistent Mathematics or Domain Theory. I will address these various incarnations as to their role, later. The problem is -- if mathematics is anything, it is a formalism – a representation. But in fact it is more, it's a language – and that language is about “numbers” but in a more general sense – it's about “information,” so computer science and mathematics are intimately related. In fact, one could argue that mathematics is a poor man's version of information science (a more proper name for computer science), for it is missing a good sense of "process." In particular, mathematics does not handle the notion of semantic notion of "random" very well, until recently with Schramm-Loewner evolution. It should be noted that the more complex the numbers, as in quaternions or octonions, the more information that is embedded implicitly. However, how much of that information is random information? And what does one MEAN by "random" -- again "random" is a "word." And what is the function of that random information as randomness becomes more solid and entangled within the complexity of a mathematical "system" such as conventional propositional logic or Rn space?
As a start, there seems a balance of information between order and disorder when generating mathematical ideas and looking at their consequences. Gregory Chaitin has shown that within number theory some facts (or "theorems") are essentially "random." That is, there are statements that are "true" (or "in" the language) that cannot be reduced or abstracted. Junctional logic(the elements 0,1, and only the AND ^ operator) -- a meet-semilattice --, although simple, sound, consistent, and "complete" (to a degree, explained later), the power of this logic is found to be not very interesting, even to mathematicians who typically don't care about "meaning." Too much order is not interesting, however, too much chaos is considered unmanageable (or too complex).
Abandon the Shannon
I am interested mathematics from a global informational and semantic point of view. Of course, some would immediately ask what about Chaitin complexity, or Crutchfield's approach, or even Shannon information. All of these approaches are important and I will eventually put them in context. However, to be brief, I am not primarily interested in algorithmic complexity, Shannon information, or the 32 other kinds of complexity Seth Lloyd enumerated, because they assume “loss or gain of information” without a rich context as a primary criteria in representation. One may think this is a bad rap, a glib strawman characterization on my part, but for now I ask you to suspend your suspicions, in this regard, for a while. I will explore the notions of material complexity, functional complexity and lastly comparative complexity. Essentially, I am more interested in “change in information” from two perspectives, “replication” and “dissipation” concentrating on the functional and comparative role, given the structural role as been the primary "way" science and mathematics has been successful. To explain what I mean by that last relatively obscure sentence, I need to delve into mathematics, physics, biology, computer science, and their history.
The problem is the “fabrication of mathematics” -- that construction and destruction of mathematics is both highly arbitrary and highly constrained… What do I mean by that? I will try to explain this in the ebook, but for now I will introduce a story about normed division algebras, that I think illustrates the circle of ideas that encompass the issue.
The interplay between tensors, a generalization of vectors, and the form of normed division algebras, is an interesting story to examine. It will take a few chapters to explain this, for this is the crux of the problem. To give you a flavor what I mean, in the realm of mathematics, I will briefly examine some of the pre-history of the concept tensor, and the opposing roles of W.R. Hamilton and Oliver Heaviside.
The quickest way to broach this problem is to quote John Baez, taken from his paper Octonions. He provides a small hint why Gibbs and Heaviside's "workmen" methods over took Hamilton's more well-founded methods, and again this is the crux of the matter. First, Baez introduces Hamilton and his follower's discoveries regarding some properties of the normed division algebras.
There are exactly four normed division algebras: the real numbers (
), complex numbers (
), quaternions (
), and octonions (
). The real numbers are the dependable breadwinner of the family, the complete ordered field we all rely on. The complex numbers are a slightly flashier but still respectable younger brother: not ordered, but algebraically complete. The quaternions, being noncommutative, are the eccentric cousin who is shunned at important family gatherings. But the octonions are the crazy old uncle nobody lets out of the attic: they are nonassociative.
Most mathematicians have heard the story of how Hamilton invented the quaternions. In 1835, at the age of 30, he had discovered how to treat complex numbers as pairs of real numbers. Fascinated by the relation between
and 2-dimensional geometry, he tried for many years to invent a bigger algebra that would play a similar role in 3-dimensional geometry. In modern language, it seems he was looking for a 3-dimensional normed division algebra. His quest built to its climax in October 1843. He later wrote to his son, ``Every morning in the early part of the above-cited month, on my coming down to breakfast, your (then) little brother William Edwin, and yourself, used to ask me: `Well, Papa, can you multiply triplets?' Whereto I was always obliged to reply, with a sad shake of the head: `No, I can only add and subtract them'.'' The problem, of course, was that there exists no 3-dimensional normed division algebra. He really needed a 4-dimensional algebra.
Of course there is much more to the story, but again this does not concern us at the moment. The important battle that ensued gives us a clue at a problem. Again for brevity, I quote John Baez, again from his paper Octonions.
One reason this story is so well-known is that Hamilton spent the rest of his life obsessed with the quaternions and their applications to geometry [ 41 , 49 ]. And for a while, quaternions were fashionable. They were made a mandatory examination topic in Dublin, and in some American universities they were the only advanced mathematics taught. Much of what we now do with scalars and vectors in
was then done using real and imaginary quaternions. A school of 'quaternionists' developed, which was led after Hamilton's death by Peter Tait of Edinburgh and Benjamin Peirce of Harvard. Tait wrote 8 books on the quaternions, emphasizing their applications to physics. When Gibbs invented the modern notation for the dot product and cross product, Tait condemned it as a ``hermaphrodite monstrosity''. A war of polemics ensued, with luminaries such as Heaviside weighing in on the side of vectors. Ultimately the quaternions lost, and acquired a slight taint of disgrace from which they have never fully recovered [ 24 ].
So the question really is: why did a more "ad-hoc" methodology of vectors (that hermaphrodite monstrosity in Tait's terms) overwhelm the “nice,” and “neat” well-founded normed division algebras? The answer, in part, is that “vector algebra” in the form of “tensors” is more flexible at the representing what people wanted. Being restricted to 1, 2, 4, and 8 dimensions was confining. In this particular case, it was the physicists, such as Gibbs and Heaviside, who “won” out. The classic case of the power of tensors was illustrated in the early part of the 20th century by Einstein's field equations, a tour de force in tensor calculus. The bottom line is that tensors are a generalization of numbers, and there lies both their strength and their weakness. Normed division algebras are both are a generalization and a specialization of numbers, and that is their strength and weakness too.
However, tensors will not entirely escape the specialization trap. The sameness of randomness will invade higher order tensors, just as all other forms of mathematics, like the normed division algebras. Pythogoreans uncovered a hint of this kind of "problem," a long time ago in the form of the "irrational number." The last hint of the mystery between generalization and specialization that comes from the Octonions is as follows. Again, I quote John Baez from Octonions.
The octonions also have fascinating connections to topology. In 1957, Raoul Bott computed the homotopy groups of the topological group
, which is the inductive limit of the orthogonal groups
as
. He proved that they repeat with period 8:
This is known as `Bott periodicity'. He also computed the first 8:

Note that the nonvanishing homotopy groups here occur in dimensions one less than the dimensions of
, and
. This is no coincidence! In a normed division algebra, left multiplication by an element of norm one defines an orthogonal transformation of the algebra, and thus an element of
. This gives us maps from the spheres
and
to
, and these maps generate the homotopy groups in those dimensions.
The visuallization of higher dimensional manifolds, more than three dimensions, is difficult. However, as it turns out that some aspects, such as topological complexity, gets simpler, such that strings (one dimensional manifolds) which can (and often do) knot in three dimensions, can unknot in four dimensions. The worms (and strings), in some sense, open up in higher dimensions. On the other hand, the vague notion of "independence" becomes "complicated," in higher dimensions. For example, in 4-dimensional Euclidean space, the orthogonal complement of a line is a hyperplane and vice versa, and that of a plane is a plane. Something is rotten in Denmark (or at least, starting to rot or smell of worms). Notice, orthogonality, a concept related to "independence" or "degree of freedom" is a key concept in homotopy groups. The dimension number determines the homotopy groups, but the dimension is 'suppose to represent "independence"' from other dimensions in tensors, clearly that is not the case. The order of these dimensions matters, as Bott periodicity indicates (or maybe it is better to say, ordinality matters, just as much as cardinality).
"They were telling me how chaotic it was and they said, 'It's such a mess; Murray [Gell-Mann] even thinks that it might be V and A instead of S and T for the neutron [decay]' I realized instantaneously that if it would be V and A for the neutron [decay] and if all the decays were the same, that would make my theory right. Everything is V and A, nothing to it!" Richard Feynman [The Beat of a Different Drum, p465] ... my emphases
Complexity is a broad and confused term: there are many forms: effective complexity, algorithmic complexity, logical depth, Krohn-Rhoades, to name a few. It will be argued that only one criteria, one level, or one metric -- one semantic: numbers, will not suffice in looking at how natural systems and mathematical language should be characterized. On the otherhand, the chaos and order of mathematics, computer science, logic, and science needs some more of a systematic, abstract but meaningful, and precise way of constructing and deconstructing. In other words, like Galileo implied: two new sciences of fabrication are needed: Comparative Science and Relational Complexity.
For example, what are the advantages of the Hamiltonian approach to the Lagrangian approach, in terms of complexity? They both have their advantages and disadvantages. Richard Feynman learned the Lagrangian approach and then the Hamiltonian approach, thinking that the Hamiltonian approach was superior. He later changed his mind. The Lagrangian approach was more flexible, and Richard was familar with, and smart enough to use it to good effect. The newer, more conventional Hamilton approach, is more structured and easier to use in "simple" situations. But both of the approaches, essentially, assume equilibrium, in a very technical sense. They are fine techniques, in their LIMITED way. What about in non-equilibrium situations, which is every thing in the world.
If you aren't going fishing, don't open a can of worms.
David West Keirsey
This story of the tension between generalization and specialization is more complicated, however, so one has to widen one's perspective in the good and bad sense, and this story takes us beyond the pale of mathematics and 20th century physics. We must visit some history of biology and life, along with visiting some other 20th century physics that opened another can of worms, namely Max Planck's bombshell of the quanta, introduced in 1900. Moreover, we must delve deeper into mathematics also, as the mathematical biologist, Robert Rosen, has said:
I feel it is necessary to apologize in advance for what I am now going to discuss. No one likes to come down from the top of a tall building, from where vistas and panoramas are visible, and inspect a window-less basement. We know intellectually that there could be no panoramas without the basement, but emotionally, we feel no desire to look at it directly; indeed we feel an aversion. Above all, there is no beauty; there are only dark corners and dampness and airlessness. It is sufficient to know that the building stands on it, that it supports, its pipes, and the plumbing are in place and functioning.
In the simple act of adding two numbers, which we are taught as children, one does not really think much about it. Think about it. 1 + 1 = 2. Ok, big deal. But there is something not noticed here, because it is so basic we don't think about it. In computers, the = sign of Fortran was replaced by the assignment operator (e.g., :=) and the equal sign predicate operator (e.g., ==) in other "newer" languages such as Algol to avoid the semantic confusion in the computer language. The point being assignment is not the same as equivalence. When one does an operation, one eliminates the operator (in some sense, it is destroyed: the operator dies), in that very act. This distinction, this act, is very important in modelling and language, for the information theoretic and semantic implication of this subtly, I think has not be explored enough. For "death of an operator" is not as final as it seems. Any operator is "work" and "information" of that work does not disappear, even Hawking has admitted that. So where did that information go? In some black hole? In the increase in the universe's entropy? Clearly the result of the operator, some of the information about the operator can be inferred, and result has some mutual information. Lloyd and Pagel's thermodynamic depth and Charles Bennett's logical depth touches upon this issue, but not in the right way, because the lack of their attention to semantics. The problem regarding the relations between function (in its general meaning) versus structure in mathematics, needs to be explored.
This isn't right, this isn't even wrong.
Wolfgang Pauli
We are all agreed that your theory is crazy.
The question which divides us is whether it is crazy enough to have a chance of being correct.
My own feeling is that it is not crazy enough.
Niels Bohr
One might have to talk about the fact that the finite is infinite and the infinite is finite. What?! That's crazy talk, as my father would say. My reply is, of course, yes, but is it crazy enough? Kant rolls over in his grave, and Hegel sits up and smiles. The real question is what are the key relations between the infinite and the finite, besides no relation, complement, and commonalty?
Rene Thom had said:
Relations with my colleague Grothendieck were less agreeable for me. His technical superiority was crushing. His seminar attracted the whole of Parisian mathematics, whereas I had nothing new to offer. That made me leave the strictly mathematical world and tackle more general notions, like the theory of morphogenesis, a subject which interested me more and led me towards a very general form of 'philosophical' biology.
Again.
There are two ways to do great mathematics. The first is to be smarter than everybody else. The second way is to be stupider than everybody else—but persistent.
Raoul Bott
I am definitely not as clever as guys like von Neumann or John Milnor (or thousand of others), but they have been restricted by their time, place, and interests. Luckily, now the Internet has created the next level of complexity - both INFORMATION and EXFORMATION. And I am persistent in the exploring of that. I am a Viking Reader of books and people.
Where there is matter, there is geometry.
Johannes Kepler
God made the integers, all else is the work of man.
Leopold Kronecker
What I cannot create, I cannot understand.
Richard Feynman
"If we are honest – and as scientists honesty is our precise duty" -- Paul Dirac
Again to give an indication of a problem, let us look at the fields of string theory and loop quantum gravity from on high, before we plunge into the depths. That high perch partly being a function of time.
In relatively recent ancient times, the Greek astronomer Ptolemy devised a method to model the heavens -- those pinpoints of light in the night sky. The problem came in that there were “wandering stars” and these things, called planets, seemed pretty predictable, but not completely. In fact, Ptolemy had to devise a pretty complicated model using his “perfect” and "simple" circles by including the notion of epicycles. Through sheer doggedness, he “fit” these paths of the planets and provided mariners and clerics, useful tables that were “good enough for government work” that held sway for about 1300 years.
Of course, along came Copernicus, who suggested a better model, which was instantiated, modified, and refined into mathematical form by Kepler, and then converted and generalized into a simple differential equation by Newton. Newton, in creating and applying calculus, started the trend in using simple to sophisticated differential equations to model the world. Bernoulli, Lagrange, Riemann, and others continued the process in the development of a kind of implicit recursive function theory in modeling physical processes and mathematical sequences.
More recently, in the 1800's physicists have used mathematical methods, namely the Fourier transforms and the Taylor series as general “fitting” strategies. It is well known that one can approximate any single line curve using either a Fourier or a Taylor series, given enough terms (with real coefficients). This strategy, the strategy of building up a model by cobbling together a set of mathematical pieces -- is similar to Ptolemy's strategy. It should be pointed out that Newton's laws of motion are essentially a two-term cutoff of a Taylor's series expansion of 1/(x-1)[Chapter 4, Life Itself]. Slightly more complicated version of Newton's laws, Lagrangian and Hamiltonian differential equations have been the mainstay of much of physics. Renormalization groups, a range-limited form of differential equations (there is a scale cutoff) is yet another form of these kinds of recursive functions even more sophisticated. Of course, there was a crisis in physics that started to brew with Max Planck's discovery of quanta in the domain of the very small and Einstein's discovery of relativity in the domain of the very large.
There is a problem here, of course, what does one mean by "large" and "small" and what is the relationship between those concepts and "in" and "out".
Tensors, the next step in mathematics proper, is a next generalization of differential equations using recursive function theory in multiple dimensions. Werner Heisenberg's quantum mechanics in the form of non-communitive matrix algebra was shown to be "mathematically equivalent" by Erwin Schrödinger wave mechanics, a recursive function formulation. Both men were hoping this method of modeling would have the Church/Turing thesis to be true. Unfortunately, Church's thesis is not true [Rosen 91]. Mathematically, Paul Dirac came up with a simple trick, which helped both Heisenberg and Schrodinger "bridge" the quantum gap. Semantically Dirac's hack didn't work as well, after a couple of decades: adding up measures still left you with measures, WHAT is THE POINT? Well, THE POINT (the particle) is the point, a very specific form of measure. In-form-ation
"What is crucial here is that we are calling attention to the literal meaning of the word, i.e. to in-form, which is actively to put form into something or to imbue something with form." -- Bohm, D. (2007-04-16). The Undivided Universe (Kindle Locations 1018-1019). Taylor & Francis. Kindle Edition.
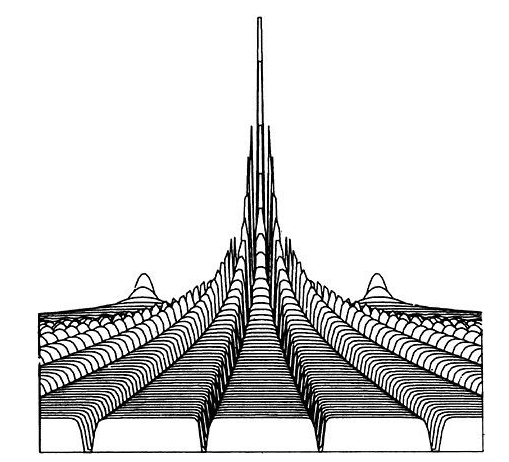
Quantum Potential
David Bohm had difficulty with the conventional physics of the likes of Schrodinger, Dirac, and Bohr. In his view, subatomic particles such as electrons are not simple, structureless particles, but highly complex, dynamic entities. He rejected the view that their motion is fundamentally uncertain or ambiguous; they follow a precise path, but one which is determined not only by conventional physical forces but also by a more subtle force which he calls the quantum potential.
Meanwhile, the main stream physics community, such as developers of QED and QCD and including string theorists, have continued to believe in Quantum Mechanics as useful mathematical representation which has a very accurate heuristic simulation below the Planck wall, and not worrying too much about a possibility of an understandable ontological model of the Planck landscape.
Quantum mechanics, with its leap into statistics, has been a mere palliative for our ignorance -- Rene Thom
In some sense, similar to Riemann's dreams, tensors are a general way of adding dimensions to the modeling problem whether the dimensions be large in the case of Einstein's relativity or small in the case of Planck's quanta. In the final analysis, similar to Ptolemy, it is now hoped by modern string theorists that cobbling together enough “dimensions” and in the right way (26 or less – 11 seems particularly attractive at this point) they can model the universe: large or small. The technical term for this wish is called M-theory.
String theory started from a basis of the Gamma function in the form of the Beta Function. The Gamma function could be viewed as a more sophisticated function to model things than the Fourier or Taylor expansion, being more complicated. Leonard Euler was the first to demonstrate that the Gamma Function can operate naturally on the complex plane. (Remember the previous discussion on normed division algebras). Whereas the Taylor expansion does not immediately suggest itself in more sophisticated connections (such as higher forms of normed division algebras) between dimensions. It should be noted that the Gamma function is a meromorphic function (essentially it can canonically cover a surface, with holes -- think replication and dissipation).
|
|
|
(1) |
|
|
|
(2) |
The interesting part of Gamma function is its both analog and digital nature. Viewing z<0 the value of Gamma alternates in between positive and negative infinity having “poles” at the negative integers. Using complex numbers as an argument, one can span both the realm of the large and the small with an interesting notion of the 2D manifold. The Beta function expands on this and can be extended in modeling by adding time (as a modeled by a single Real Number) and quantum numbers to model complex dynamic strings -- in some sense, adding tensor columns or rows to create enough state for your favorite physical phenomena. The "positive" plane can serve as modeling "replicative" processes whereas the "negative plane" can serve as modeling "dissipative" processes, entangled (by the square root of -1) nonetheless. The simple product ab is entangled in a certain way, and so is a +bi but in a different way. So what determines what is entangled and in what way?
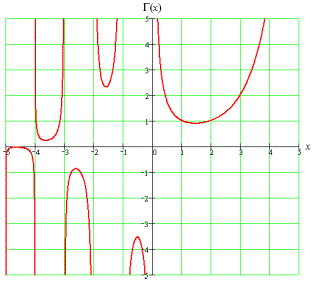

Limiting oneself to only 10, 11 or 26 dimensions, seems like a shame.
And in fact, the current Standard Model of physics has boiled things down to about 26 “constants,” or “parameters” with physicists hoping to make that number smaller. But, why not use 100 or a thousand constants or dimensions -- the more the better? Why not hundreds of quantum numbers -- let's throw in a bunch. Why not try to use the Monster group as a model? (Actually there is a good reason for using the Monster, but the reason is "complicated"). Let's get entangled.
Of course, Occam's razor raises its head, in this case – the response would be from physicists -- how dare you -- complicate the model, for no reason. Of course, Physicists are right to look at Occam's razor -- the only problem is, however, using 11 dimensions in certain ways is just one way to “complicate” the model. What justifies their complication to 11 dimensions? There are an infinite number of ways to "complicate" a mathematical model from let us say three dimensions to eleven dimensions using the notion of tensors. There are many ways of entanglement. And they aren't equivalent from an information theoretic (and semantic) way.
A problem lies here in exactly what is meant by “complicating” the model. It turns out there are an infinite number of ways of “complicating” a model mathematically, and that is a problem, when it comes to modeling.
One major problem is making clear what the relationship is between the “models” and the thing or things being modeled. For example, consider the question, what is -- a relationship between the use of dimensions in string theory and using “constants” in the Standard Model in terms of mathematics?
To see this issue of multi-paths of complication, let us “try” to complicate a simple mathematical model as much as we can, and see what happens. The classic method in mathematics is to “go to a higher dimension,” and see what one can see. In this case we will look at “simple” mathematical objects: the circle, the triangle, and the square. Let us take our handy real numbers ![]() , create some copies and form a Euclidean space
, create some copies and form a Euclidean space ![]() n. Now we can gradually increase n, from 1,2,3,4,5,6, … to infinity. If one looks at “surfaces” (or more generally manifolds) in these “spaces” there are some curious things that happen, that may seem counterintuitive at first. First, consider the surface area of a unit n-dimensional square – a “hypercube.” As one increases the unit hypercube dimension, the total surface area of hypercube gets bigger. This seems, as it should be. The surface area of unit hypercube, as N goes to infinity, the area goes to infinity. However, let us consider something “smaller” than a unit hypercube, but fairly simple: the unit n-dimensional circle – a “hypersphere.” As N increases from 1 to 2 to 3 to 4, the surface (and volume) of the unit hypersphere increases . This seems, as it should be. However, between dimensions 5, 6, 7, and 8, something kind of weird happens. The surface area of the hypersphere starts decreasing. Now, conceptually this initially does not make sense. If one increases dimensions, wouldn't the surface area of a figure, with more dimensions, INCREASE, as the hypercube does? But looking at the formula, clearly this is not the case in the hypersphere. In fact, at limit of infinite dimensions, the surface area of a hypersphere is zero. Moreover, the volume of a hypersphere goes to zero, and all other manifolds of a hypersphere. Clearly a curved surface is different from a planar surface – and that seems to effect volume or higher dimensional manifolds.
n. Now we can gradually increase n, from 1,2,3,4,5,6, … to infinity. If one looks at “surfaces” (or more generally manifolds) in these “spaces” there are some curious things that happen, that may seem counterintuitive at first. First, consider the surface area of a unit n-dimensional square – a “hypercube.” As one increases the unit hypercube dimension, the total surface area of hypercube gets bigger. This seems, as it should be. The surface area of unit hypercube, as N goes to infinity, the area goes to infinity. However, let us consider something “smaller” than a unit hypercube, but fairly simple: the unit n-dimensional circle – a “hypersphere.” As N increases from 1 to 2 to 3 to 4, the surface (and volume) of the unit hypersphere increases . This seems, as it should be. However, between dimensions 5, 6, 7, and 8, something kind of weird happens. The surface area of the hypersphere starts decreasing. Now, conceptually this initially does not make sense. If one increases dimensions, wouldn't the surface area of a figure, with more dimensions, INCREASE, as the hypercube does? But looking at the formula, clearly this is not the case in the hypersphere. In fact, at limit of infinite dimensions, the surface area of a hypersphere is zero. Moreover, the volume of a hypersphere goes to zero, and all other manifolds of a hypersphere. Clearly a curved surface is different from a planar surface – and that seems to effect volume or higher dimensional manifolds.
Hypersphere
Dimension |
Volume |
Area |
1 |
2.0000 |
2.0000 |
2 |
3.1416 |
6.2832 |
3 |
4.1888 |
12.5664 |
4 |
4.9348 |
19.7392 |
5 |
5.2638 |
26.3189 |
6 |
5.1677 |
31.0063 |
7 |
4.7248 |
33.0734 |
8 |
4.0587 |
32.4697 |
9 |
3.2985 |
29.6866 |
10 |
2.5502 |
25.5016 |
The implication of a hypersphere surface in higher dimension going to zero is that somehow “chaos” is encroaching into the surface and the volume, and all other derivations of higher dimensions of “volume.” Where as looking at the hypercube, the “surface” becomes infinite “order”(the measure goes to infinity) but the volume stays the same magnitude, equivalent to “1”. So the issue becomes what are the relations between “chaos” and “order” in mathematics. Maybe the relationship between measure and dimension needs examining. For example, there is a question of why does the surface area of a hypersphere peak at seven dimensions and why does the volume peak five dimensions?
The notion of "measure" becomes problematic once there is more than one "dimension" in one's measure. In finite linear Euclidean spaces, the issue does not raise its interesting but difficult head: the simple notions of eigen functions and eigen values seem to "cover" the metaphorical "space." As long as there is a simple linear relationship between the "dimensions," there is a relatively simple (?linear and global?) metric. On the other hand, with the discovery of non-Euclidean metrics and the associated concepts of non-Euclidean geometry and Ricci curvature, which have not been widely taught or infused into many mathematical or scientific areas, such that the logical and scientific ramifications have yet to really be addressed fully.
On the other hand, thinking about it, the relationship between the hypersphere and hypercube as the number of dimensions increase is not as mysterious as it appears. The unit “measure” of the hypercube is, in some sense, “orthogonal” to the unit “measure” of the hypersphere. As the dimensions increase, the hypercube unit measure is exactly “replicated” in each dimension (the linear metric is common), whereas the unit measure of the hypersphere actually is equally “dissipated” (shared) in each dimension. However, it is a little more complicated regarding other n-dimensional polytopes, because once the "measure" is mixed (replicated and dissipated) between "dimensions," non-linear effects confuse the issue.
To illustrate this, first, there is another simple kind of manifold that is similar to the hypercube; it's the hypersimplex. The hypercube comes from the square and the hypersimplex comes from the triangle. The interesting thing about the infinite dimension unit hypersimplex (where the unit is the measure of the surface area of the 2D triangle) is the volume goes to zero, but the surface area goes to infinity. How can that happen? What is going on with this “measuring.” How can an infinite surface area come from a zero volume manifold? The obvious inference in this is the more dimensions that “share the space” the space is spread around, even though "dimensions" are “independent” or at least "orthogonal." Hilbert's Hotel exposes its "ghost." This “replication” of this unit measure is a little more complex. There is another indication of the problem, based on the Banach-Tarski paradox.
A Unit Hypersphere (r=1) |
A Unit Hypersimplex (1/2bh=1) |
The Unit Hypercube (b=h=1) |
|
Manifold 3-D Volume at the limit of Infinity |
0 |
0 |
1 |
Manifold 2-D Surface Area at the limit of Infinity |
0 |
Infinity |
Infinity |
Second, despite the fact that these mathematical forms (polytopes and hyperspheres) is embedded in linear Euclidean spaces, surface and volume increase in the lower dimension hyperspheres so the “dissipation” is cannot be simple, the relationship between “numbers” (the elements of the space) and the “space” is important. There is much more details in the “dissipation” of the hypersphere unit metric. The bottom line is there no perfect “replication” or “dissipation” – they are entangled, and how they are entangled depends what kind of elements and operators on those elements that are defined within the dimensions (and spaces) and how they relate between dimensions and spaces. What kind of destruction (and construction) are those operators doing, when they are living and dying, or Working.
But what is a "dimension" and a "space"? In fact, what is the definition of a "number"?
Tables, chairs, and beers mugs must be able to be substituted for points, straight lines, and planes.
David Hilbert
An Example?! ... A Specific Example!? ... Ok, take the prime number 57.
Alexander Grothendieck
2.1.4 A Problem with Mathematical Words: Number, Dimension, and Space
Although mathematics is primarily about numbers, mathematicians must convey their definitions and ideas partially through natural language, for not all mathematical objects can be defined rigorously (strictly in terms of other defined objects). Moreover, the simple words, such as "in" and "out" are used to, but what do they "mean." For example, in Euclidean geometry, the concepts of point, line, and plane cannot be defined in terms of other more primitive concepts. Moreover, sometimes the naming of mathematical concepts can be less than clear; in fact, sometimes they are downright confusing. For example, consider the concepts of Gaussian and Eisenstein integers. One would assume that these kinds of numbers are “kinds of Integers.” However, a Gaussian integer is not a “Real number” as all Integers are, but is a “Complex number.” A Gaussian integer is complex number in the form a + bi where a and b are integers and i= sqrt(-1). An Eisenstein integer and more quaternion notions such as Lipschitz and Hurwitz integers are similar in their misleading names. Although it is clear that the mathematical definition of Gaussian integer (really a kind of an ideal) is not an integer and there is no real "confusion" in this case; HOWEVER, there are more subtle situations where there can be confusion. For example, what would an Octonion notion of "integer"[pages 100-101] mean?
When is a skew field not a field? And who decided to regard the set {0,1} over the field F2, a space (yeah, an affine space).
Mathematics is considered the most precise form of a language. Mathematics is primary about “numbers” – but in reality there is no definition of “number.” Consider that “real numbers” include “irrational” numbers. However, an irrational number is a number that cannot be expressed as a fraction p/q for any integers p and q. Notice there is a problem here. This is a recursive definition of a negative concept. There is not delineation of the concept of number. That is not very precise, to say the least. One might be convinced with more precise or complicated definitions. One can consider more rigorous definitions of things, such as defining a “real number” as a completion of an infinite Cauchy sequence. Or as Dedekind did, a Dedekind cut, a partition into two infinite sets of rational numbers. But what is a sequence? What is a Cauchy sequence? What is a set? What is a infinite set? What is a number?
One might think one is on firmer ground by more sophisticated definitions, but Hilbert was wrong, one cannot eliminate "meaning" (or non-defined "semantics", that is some "undefined" concepts as primitives) from mathematics, without it becoming trivial. Kronecker and Brouwer have asked embarrassing questions of the foundations of most of sophisticated (or even mundane) mathematics. The foundations of mathematics have been shaken and underminded ever since Cantor and Gödel had opened their cans of worms.
In Euclidean geometry, there will always be some primitive concepts that cannot be defined because one must eventually use words to refer to the “real world” concepts mentioned. Even in a more rigorous definition, a primitive concept such as “sequence” must be assumed to be understood or a few examples are given (like in the examples of “dimension” and “space”). There will always be a set of “primitive” concepts for any formal system proposed. And it is assumed that everybody involved “understands the meaning” of these concepts. Unfortunately, that assumption is not always true. It took approximately 2100 years to question the notion of the seemingly rock solid word "space" from Euclid to Lobachevsky to Beltrami. If we are not sure what "space" is, then what about the words, "in" and "out?" Well, it all depends on what "is" -- "is." What is the difference between a mathematician and lawyer? -- One knows he is lying or obscuring.
Moreover, the basic word "number" thought to be "simple" is in actually very complex. As it turns out the meaning of the word “number” started to change significantly for mathematicians in the 17th century [page 9, Pesic 2003]. The concept of number held by the ancient Greeks (arithmos) and the layman was primarily what we call “counting numbers” or “natural numbers” (in modern notation N ) was no longer in force or separate from magnitude (megethos). The ancient Greeks, did not consider "one" (1) as a number, let alone zero as a number. Nevertheless, as mathematics progressed in algebraic sophistication, the notion of “number” has implicitly expanded, including concepts such as zero, binary numbers, negative numbers, rational numbers, algebraic numbers, irrational numbers, transcendental numbers, "real" numbers, complex numbers, Cayley numbers, ordinal numbers, transfinite cardinal numbers, Betti numbers, etc., such that the notion of “number” became more general and specific, way beyond a layman's notion of “number.” Complicated numbers (e.g. anything but 1) really include complicated operators implicitly. As computer hardware engineers know, the implementation of the simple operator addition, can be very complex, which usually uses the convenience of twos-complement logic rather than the straight forward combination of concatenation, and the boolean operators Xor, And, and Or. Even integers are limited to an approximation within the computer (that is, each integer has an "approximating" finite limit of bits for representation, which works as long as the numbers don't exceed the limit). Computer implementations must include a semantic "overflow" bit to handle the exceptions. Theoretically the computer cannot represent integers, because they implicitly include the notion of infinity; however, the computer can represent the operations on many integers(more than any human), and they can represent most of simple abstract operations on integers, like addition or twos complement. There are complex operations, such as division, have exceptions (like division of zero or underflow), so one can create sentences or symbols that have no "value" or "meaning" (or ambiguous meaning), unless directly assigned by the encompassing formal system. (e.g., the computer hardware and microcode).
Nevertheless, we all seem to have one sense of number: the ability to count. On the other hand, there is a seemingly related notion of “measure”: where counting is the basic kind of measure, whereas “ratio” is another regarding counting and comparing. The problem comes when there is some form of “incommensurate” situation or “uncountable” as another. How can a number be “incommensurate” (unmeasurable, hence incomparable) and “uncountable” and still be a number? Transcendental numbers, such as pi, e, gamma can be expressed as examples, but part of their expression involves the notion of infinity. Infinity is unmeasurable and uncountable. Another odd example, Gregory Chaitin defines Omega, a number that can be "defined" but not "computed."
There is a relatively "new" word that is related to "measure" -- it is "metric." A metric is a distance function that is a function which defines a distance between elements of a set. According to Wikipedia, the mathematical concept of a function expresses dependence between two quantities, one of which is given (the independent variable, argument of the function, or its "input") and the other produced (the dependent variable, value of the function, or "output"). Notice this "definition" is a bunch of words, including "quantities" (back to that "thing" number). The word "metric" sometimes refers to a metric tensor.
The methodology of incorporating different kinds of infinity (such as axiomatic definitions of rings and fields), although it greatly expands our knowledge and power of mathematics, but in some sense we lose some control. There are supposedly more transcendental numbers than all other numbers, but they cannot be enumerated or measured. Propositional logic, equivalent to the N, is the “simplest complex” formal axiomatic system for it is one of the last complete, sound, and consistent theories, and practically anything beyond is too complex. That is, a interesting mathematical system can be complex(complicated), sound, and consistent, but it cannot be complete. On the other hand, Tarski has proven that a theory of a real field is decidable, whereas the "simpler" ring of integers is not decidable. So what is "simpler" or "more complex"? The real line and normal calculus is in some sense "easier" than dealing with diophantine equations, which are limited to "just" integers.
Number theory, although powerful, has random elements as part of its meaning. [Chaitin 2001] The mathematicians Leopold Kronecker and LEJ Brouwer had major objections to this non-constructive view of mathematics because of this problem, and their questions have never been successfully answered.
A similar problem of ambiguity occurs with the notion of dimension. There is no definition of dimension, except in a recursive manner. For example, consider the following from Mathworld. My emphasis in bold italics is added.
Dimension is formalized in mathematics as the intrinsic dimension of a topological space . There are several branchings and extensions of the notion of topological dimension. Implicit in the notion of the Lebesgue covering dimension is that dimension, in a sense, is a measure of how an object fills space. If it takes up a lot of room, it is higher dimensional, and if it takes up less room, it is lower dimensional. Hausdorff dimension (also called fractal dimension ) is a fine tuning of this definition that allows notions of objects with dimensions other than integers. Fractals are objects whose Hausdorff dimension is different from their topological dimension.
Notice, the definition of “dimension” is vaguely pointed to as a form of measure, but it is primarily referred to itself (?"dimension is dimension"?).
The notion of mathematical "dimension" has become as sophisticated as number, way beyond the layman's view of dimension. The following are examples of mathematical definitions using the notion of dimension.
Capacity Dimension , Codimension , Correlation Dimension , Exterior Dimension , Fractal Dimension , Hausdorff Dimension , Hausdorff-Besicovitch Dimension , Kaplan-Yorke Dimension , Krull Dimension , Lebesgue Covering Dimension , Lebesgue Dimension , Lyapunov Dimension , Poset Dimension , q -Dimension , Similarity Dimension , Topological Dimension , Vector Space Basis
The notion of dimension looks to some degree related to the notion of space, but in mathematical terms the notion of space is also undefined. According to Mathworld:
The concept of a space is an extremely general and important mathematical construct. Members of the space obey certain addition properties. Spaces which have been investigated and found to be of interest are usually named after one or more of their investigators. This practice unfortunately leads to names which give very little insight into the relevant properties of a given space.
The everyday type of “space” familiar to most layman is called a 3D Euclidean space. One of the most general types of mathematical spaces is the topological space . On the other hand, there are a significant number of “spaces.” Not all are considered a topological space, so there is no one definition of space. State "space" typically is a significantly different concept from topological space. The following is a list of different kinds of “space.”
Affine Space , Baire Space , Banach Space , Base Space , Bergman Space , Besov Space , Borel Space , Calabi-Yau Space , Cellular Space , Chu Space , Dimension , Dodecahedral Space , Drinfeld's Symmetric Space , Eilenberg-Mac Lane Space , Euclidean Space , Fiber Space , Finsler Space , First-Countable Space , Fréchet Space , Function Space , G -Space , Green Space , Hausdorff Space , Heisenberg Space , Hilbert Space , Hyperbolic Space , Inner Product Space , L2-Space , Lens Space , Line Space , Linear Space , Liouville Space , Locally Convex Space , Locally Finite Space , Loop Space , Mapping Space , Measure Space , Metric Space , Minkowski Space , Müntz Space , Non-Euclidean Geometry , Normed Space , Paracompact Space , Planar Space , Polish Space , Probability Space , Projective Space , Quotient Space , Riemann's Moduli Space , Riemann Space , Sample Space , Standard Space , State Space , Stone Space , Symplectic Space , Teichmüller Space , Tensor Space , Topological Space , Topological Vector Space , Total Space , Vector Space
By axiomatizing automata in this manner,
one has thrown half of the problem out the window,
and it may be the more important half.
-- John Von Neumann
There is an intimate relationship between the notion of a conceptual model and the nature of inference. The first part of a conceptual model is making distinctions. Distinctions are the bread and butter of models, a main difference between models is how many distinctions are made. The second key aspect of models is the configuration: the configuration of a model determines what kind of inferencing can occur and what can be inferred. The third aspect of the model is its context: what is implicit and explicit referred to by the model. The implicit are the encodings and the decodings of symbols or propositions representing the natural system entities or a comparable formal system entities.
Formal axiomatic systems (FAS) are a kind of model of abstract conceptual models. This kind of model is very useful and has a lot of literature behind it in the last hundred years. The main problem with a FAS is there is no discipline in trying to connect natural systems (a part of reality) with the FAS. Conventional approaches in using a FAS in science are numerous as the stars. Stephen Wolfram's book an interesting, and the most recent attempt to be a more systematic applying of very specific kinds of FAS, namely automata, to reality or parts of reality.
Formal axiomatic systems, as outlined by David Hilbert refined by John Von Neumann, Alan Turing, and others, ignore the environment and the context. Moreover, the underlying composition of elements that constitute the medium in which the system is embedded is not specified.
What are the consequences of this ignoring? The general implication is that the formal axiomatic system assumes that the environment context and medium has no effect on the system. This clearly cannot be so in natural systems. Can we determine what the effect of this ignoring is? Yes, to some degree and a broad sense.
The first consequence is that a FAS cannot characterize the long-term behavior of a modeled natural system. It is guaranteed that in the long run, the “behavior” of the formal axiomatic system cannot and will not mirror a natural system. In a metaphor sense, a formal axiomatic system is a dead system and a natural system is alive.
Robert Rosen took a new perspective on FAS and natural systems. In his groundbreaking book, Life Itself, he outlines a framework for analyzing and synthesizing formal systems and relating them to natural systems. Part of this book will try to extend his framework and to create the methodology of Comparative Complexity. On the other hand, Rosen saw the creation of science as an art. I disagree with him: one can be systematic in the construction of science by being more systematic and functional in mathematics. One of the keys is incorporating systemically more "meaning," but how can we do that? Let us look at closer at the notion of entailment, and how we might connect it to "semantics" or "meaning" -- in the form of "reality."
Entailment -> en-: to put into or onto, taille: land tax imposed, -ment: result of an action or process
Dictionary Definition -- Entailment: Something transmitted as if by unalterable inheritance.
The word "entailment" has come to signify, in the context of science, a general process of deterministic linkage. Thus as Robert Rosen has said:
It is enough to observe that both science, the study of phenomena, and mathematics are in their different ways concerned with systems of entailment, causal entailment in the phenomenal world, inferential entailment in the mathematical.
Causal entailment is the realization and the reality that some phenomena follow other phenomena in our human perception and this implies that there is some regularity in the physical world. This fact about the world makes science possible. A natural system is typically a name for some idea of a part of the physical world. Causal entailment is name for the deterministic changes in that natural system.
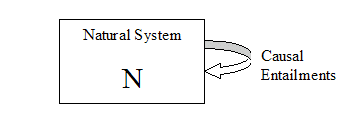
A Natural System with causal entailment
Inferential entailment is the realization and the reality that language can be used to help in reasoning: that there can be some regularity in the abstract world of ideas. And the nature of language makes both science and mathematics possible, and the fact that one can mix the two for benefit. Formal systems include a particular form of language. Most formal systems are designed for minimal ambiguity so it can use inferential entailment to maximal effect. A problem with formal systems is that one cannot eliminate ambiguity, but more the ambiguity, the more meaning can occur. The tragedy is one can create formal systems, or a corpus in the case of natural language, that have no meaning or worse, the wrong meaning.

A Formal System with inferential entailment
Entailment systems in the form of formal systems can model natural systems. Natural systems can be characterized as a system that involves causality which mirrors inferential entailment. There is a natural correspondence between causal entailment (as in causal effects) and inferential entailment. The formal system can model a natural system by encoding objects or propositions that correspond in formal system to entities or actions in the natural system. With inferential entailment, new language objects or propositions can be created. Those language objects or propositions can be decoded to correspond to entities and actions in the natural system. One very important aspect of relationship is that the encodings and decodings are unentailed, and are not part of the explicit formal system.
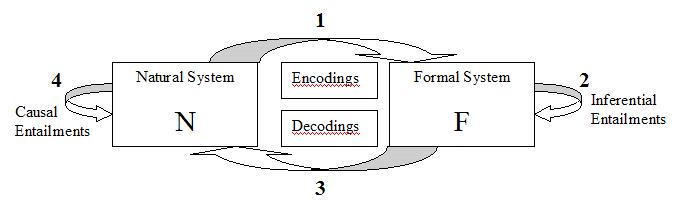
Rosen's Modeling Relation between a Natural System and a Formal System
To the degree that a formal system can reflect the natural system, the model is said to "commute." That is, to the degree, 4 = 1+2+3, one can say one has a model of N. Of course, a formal system F can never completely model a natural system N. (As side note, to some degree a natural system can "model" (2 = 3+4+1)-- or more properly -- "realize" a formal system.)
The another advantage of formal systems is that they can be compared or related to each other.
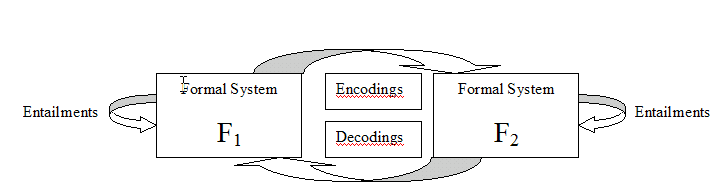
Modeling a formal system with a formal system
Formal models are composed of symbols and constitute a kind of language. The symbols and syntax can serve as encodings and decodings. Mapping symbols or syntax (or both) from one formal system to another is the decoding or encoding. When compared between two formal models, there can be assignments for encodings and decodings. To the degree 4 = 1+2+3, F2 forms a model F1, and to the degree 2 = 3+4+1, F1 forms a model of F2. Nesting of models makes chains of encodings and decodings.
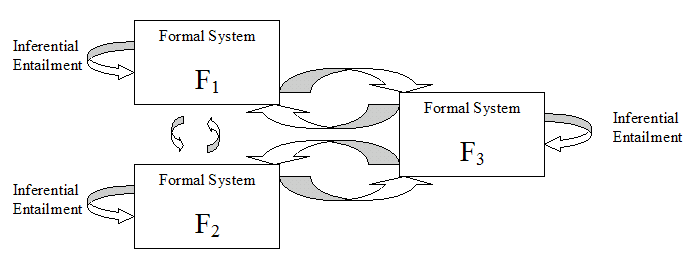
Common Formal System
When comparing two formal models, the encodings and decodings are not part of each formal system: they are not specified as part of the model. Nothing is explicit. However, one can fabricate a new formal system by including or incorporating the two formal systems together. Adding encodings and decodings as mappings (production rules) or new symbols complicates the combined model. Internalizing the encodings and decodings as rules, mappings, or symbols makes the two models and their relations somewhat explicit, although not all, for there is the inferential entailment which now is still implicit and often times, but not always in combination: sound, consistent, complete, decidable, computable, meaningful, understandable, or useful.
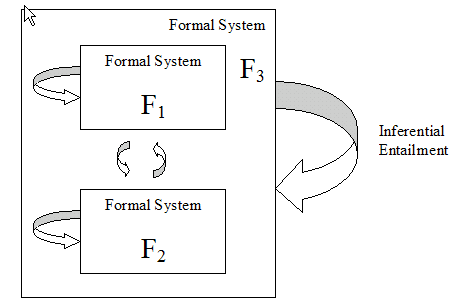
Complication: Internalization of formal systems
Consider AND boolean operator as F1 in the form of a monoid and XOR boolean operator as F2 in the form of a monoid. One result of a combination, forming a language, specifically, forming the algebra of the Field F(2) as F3.
To be more detailed, for an important but subtle point, let us consider exactly the ways this "combination" can happen. The most obvious "combination" being "obvious" but in reality one must make several implicit assumptions, in the way of being a concrete choice. And actually somewhat conventional and arbitrary in this choice, normally it is not even noticed as to the some of the assumptions. Consider the F1 and F2 tables.
|
|||||||||
|
There is no encoding or decoding between the two formal systems if we don't represent the "boolean" numbers as our elements or we don't use the same variables in the two tables. On the other hand, if one uses a particular encoding such as: a->0, c->0, b-> 1, d-> 1. IN THIS CASE, this implies a=c and b=d, although in the merged formal system F3 the equivalent (but not the same) statements (^0=•0, and ^1=•1) -- is no longer explicit (in other words encoded). In English the equivalent statement would be essentially "results of the AND operation can be used in the XOR operation, and visa versa." In computer science terminology, the results are not typed, so the operational typing is lost once operations are performed. Looking from another perspective, the resulting formal system generalizes the operators, thus effectively hiding state in the formal rules.
|
|||||||||
|
Let us get even more simple and down and dirty. Consider the notation of a function f( ). The letter f is the name of the function. All we know is that f represents or "refers" to "a function." The function can be anything, although typically the function represents "a number." But even then, the function can represent a "line" or a "surface" or even a "space," and lastly something "undefined." The canonical function is usually f(x)=y, but one can consider x(f) which is a standard trick in mathematics. Let us look the simple discrete unique combinations of the symbols (including the "blank"), given that the symbols can be equivalent except they don't have to be equal.
Of course, there are statistical methods that work very well in modeling processes and entities as in the current deep learning techniques. Artificial Neural Networks have been trying to model real things and processes since McCullogh and Pitts started in the 1930's.
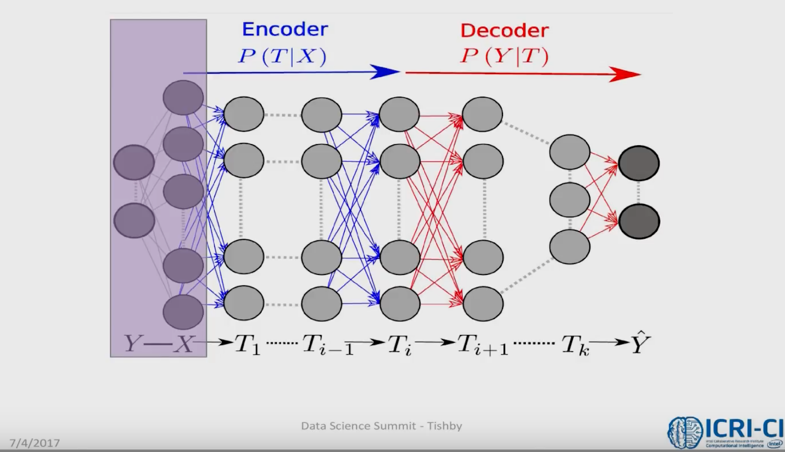
What are the relations between statistical inference and discrete information? This is a complicated question. This ebook attempts to answer that. For now, here are two stories as an introduction. Thanks I needed that! Prime

In combining or construction of two (or more) formal systems into another common formal system the resulting new formal system can either be comparable or not. In comparing, there are

Embedded encoding versus Incommensate encoding
Equivalence Relations, Smaller Model versus Larger Model
The advantages of formal systems is even more because in the natural world, the same relations can happen, just as can be mirrored in formal systems. However, we cannot "get" at natural systems explicitly, we can only refer to them by names or symbols, and operators. Natural systems are part of reality, the structural and functional organization of "reality" and can be refered to by natural language or modeled by formal systems. Moreover, one natural system can model (or realize) another natural system. The realization can be called "common organization."
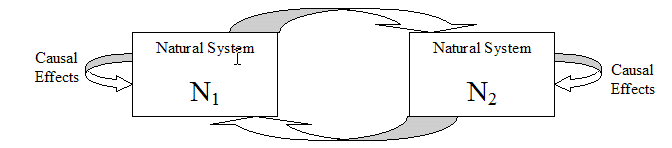
Analogy: Common Organization of Natural Systems
Assume N1 realizes part of N2, or visa versa. In otherwords, there is a common organization between them. One can model some of that common organization via a formal system.
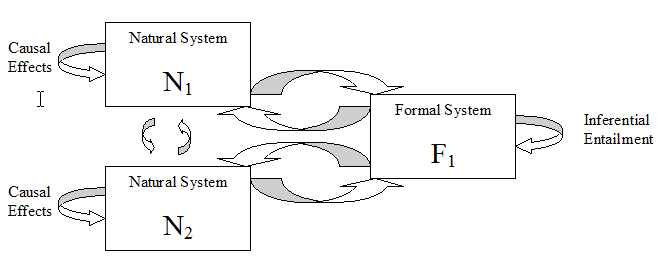
Realizing a common formal system: Models of each other.
To complicate the analysis one can fabricate two formal models to model a natural system.
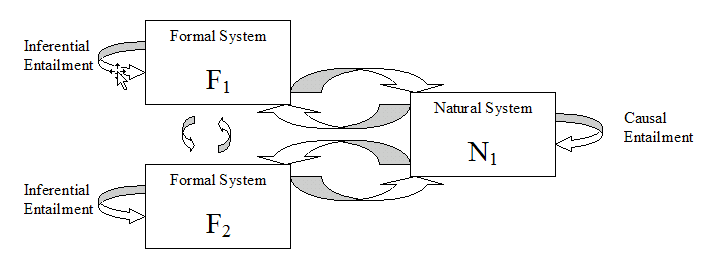
Modeling a Natural System with two Formal Systems
Framework

How to match (via analysis and synthesis) the various "models" together? That is, merging models of quantities[semantics and syntax] and qualities [semantics and syntax]. The important aspect of merging these models is to do it in a finite way, but also importantly understand the infinite contexts that will naturally replicate and dissipate into and out of the merged models so to make the "system model" - to reflect reality.
Hidden Patterns
The Standard Model of Physics
There are all kinds of models when mixing the semantic and syntactic (qualities and quantities). The key is to use those relations (combined) as a framework. The task is to use the relations of the models to derive further relations and assignments between the models, in a systemic way. Even though Quantum Mechanics' (QM) Standard Model of "particles" and "forces" (qualities) and General Relativity's model (GR) of "gravity" and "matter" (qualities) in cosmological models are both statistically based (probability and statistical measures), they shows patterns. Using a information theoretic overview, the task is to match the physical entities with forms thru discrete relations. Hence, the finite, simple Sporadic Groups, definite informational entities will serve as the Formatics Framework.
The Sporadic Group Framework
The Sporadic Group with Subquotient Links
(The 20 in Happy Family, and the 6 Pariahs)
The framework of the Sporadic Groups will serve as an overall, primary model with multiple relations between objects (e.g., Monster Group (M), Harada Norton Group (HN), Mathieu 12 (M12) and Mathieu 11 (M11)) and between all of the 27 Finite Simple Groups (including the Tits (T) Group). There are infinite number of relations between these very unique groups, and also there are 18 Infinite Classes of Simple Lie Groups, that serve in the background context. Along with other mathematical constructs (like Rings, Fields, Lattices, reduced homomorphic trees, Moufang loops, Quasiloops, Semi-groups, Monads, Cyclic Groups, Alternating Groups, Classical Groups) to match physical constructs such as particles, waves, forces, and quanta. The general physics' notions of "time", "energy", "mass", "space", "spin", "charge" will be examined very closely. We will fold, spindle, and mutilate dem' notions. They are not unitary, but simply complex and complexly simple. The Framework of the Sporadic Group (plus the Tits Group) are finitely "restricted" by the first 20 Primes as factors, which are very related to the 15 SuperSingular Primes of the Monster Group and Monsterous Moonshine.
| Mathieu 11 | (Sporadic-M11) | 7920 |
| Mathieu 12 | (Sporadic-M12) | 95040 |
| Janko 1 | (Sporadic-J1) | 175560 |
| Mathieu 22 | (Sporadic-M22) | 443520 |
| Janko 2 | (Sporadic-J2) | 604800 |
| Mathieu 23 | (Sporadic-M23) | 10200960 |
| Tits | (T) | 17971200 |
| Higman Sims | (Sporadic-HS) | 44352000 |
| Janko 3 | (Sporadic-J3) | 50232960 |
| Mathieu 24 | (Sporadic-M24) | 244823040 |
| MacLaughlin | (Sporadic-McL) | 898128000 |
| Held | (Sporadic-He) | 4030387200 |
| Rudvalis | (Sporadic-Ru) | 145926144000 |
| Suzuki | (Sporadic-Sz) | 448345497600 |
| O'Nan | (Sporadic-On) | 460815505920 |
| Conway 3 | (Sporadic-Co3) | 495766656000 |
| Conway 2 | (Sporadic-Co2) | 42305421312000 |
| Fischer 22 | (Sporadic-F22) | 64561751654400 |
| Harada Norton | (Sporadic-HN) | 273030912000000 |
| Lyons | (Sporadic-Ly) | 51765179004000000 |
| Thompson | (Sporadic-Th) | 90745943887872000 |
| Fischer 23 | (Sporadic-F23) | 4089470473293004800 |
| Conway 1 | (Sporadic-Co1) | 4157776806543360000 |
| Janko 4 | (Sporadic-J4) | 86775571046077562880 |
| Fischer 24 | (Sporadic-F24) | 1255205709190661721292800 |
| Baby Monster | (Sporadic-B) | 4154781481226426191177580544000000 |
| Monster | (Sporadic-M) | 808017424794512875886459904961710757005754368000000000 |
Hidden and Observable Patterns

Periodic Table building of atoms by nuclear processes.
Matching physical entities or processes with mathematical concepts through understanding the patterns of relationships of the frameworks, specifically, for example here are the following first 7 "largest relational concepts" as in Whole form.
| Mathieu 11 | (Sporadic-M11) | Proton | 2^4 * 3^2 * 5 * 11 |
| Mathieu 12 | (Sporadic-M12) | Neutron | 2^6 * 3^3 * 5 * 11 |
| Janko 1 | (Sporadic-J1) | Electron | 2^3 * 3 * 5 * 7 * 11 * 19 |
| Mathieu 22 | (Sporadic-M22) | Deuteron | 2^7 * 3^2 * 5 * 7 * 11 |
| Janko 2 | (Sporadic-J2) | Positron | 2^7 * 3^3 * 5^2 * 7 |
| Mathieu 23 | (Sporadic-M23) | Alpha Particle | 2^7 * 3^2 * 5 * 7 * 11 * 23 |
| Tits | (T) | Gravity | 2^11 * 3^3 * 5^2 * 13 |


Number is the within of all things.
Pythagoras
A mathematician is a device for turning coffee into theorems.
Paul Erdös
Abandon the simple Shannon, watch out for the Hamming
f a b 1) 0 1 1 2) 1 0 0 3) 1 1 0 4) 1 0 1 |
NAND operator: a | b = f(a,b)
In applying the NAND operator, one kind of “replication” is seen by the situation of line 3 and 4, when only one of the inputs is a 1, which makes the output a 1 also. In this case the replication is through time. At the same time, the operation is also one kind of “dissipation” in that only looking at the output, information is lost, and one cannot recover which input was 1. In this case the dissipation is also through time. The complete analysis of the NAND operator, in terms of dissipation and replication is more complex, and what the bits represent, of course, play a factor of what is “replicative” and what is “dissipative;” nevertheless, any kind of theoretical operation or real action in the world must be both replicative and dissipative. Although NAND is the "simplest" and in some sense one of the most transparent binary operations, it still loses information because the mapping (the operation) does not transfer the information of the operation. If the formal system has only one operation, that information can be recovered, but the order of the inputs is still lost or hidden. Replication and Dissipation must occur in any operation (encoding or decoding) or mapping.
George Boole was essentially one of the first mathematicians to look at mathematics from a radically different perspective and emphasize the notion of "operator" in the context of algebras. "Boolean" logic forms the basis for the modern digital computer and digital information. Although the original set of operators of Boolean logic is regarded as the canonical representative representation of that algebra (with the operators AND, OR, NOT), only using the NAND operator (which is the Sheffer's stroke) is an equivalent system which can serve as a full propositional logic system. Ignoring the issues of intuitionist logic, to be addressed later, boolean logic has been used as a "basis" for building computers and has resulted in possibility of the creation of the Web.
By COPYING the inputs, the other boolean operators can be ENCODED as a combination of the Sheffer's stroke. For example, the operator AND (^): a ^ b can be encoded as (a | b) | (a | b). This implicitly requires additional state (in that there are extra physical connections or "lines" in the circuit design). Mathematically using AND, OR, and NOT is just isomorphic to using the NAND. But they aren't the same (by definition), converting to a canonical representation loses certain kinds of information. Any action (including converting to canonical representations) changes the context (because either the formal axioms change or the encoding or decoding changes).
Moreover, the characterization of full propositional calculus in a canonical form as needing only one operator | is misleading. In reality, the operator Concatenation is also necessary. Concatenation is an implicit operator, part of syntax of the formal system, that puts symbols together. In construction of a sentence there is a sense of increasing the number of STATES by increasing the number of symbols in the sentence. In this regard, there is an relationship in terms of a TURING MACHINE and the system of propositional logic. The number of input symbols (and the kinds of symbols) in a propositional sentence is related to the number of symbols on the tape. It is often forgotten that with a Turing machine, there is an INFINITE amount of information included in the system AS INPUT by the fact that the tape is INFINITE in length. That a Turing machine can simulate any computation should not be surprising because there is an INFINITE amount of state, in the form of the blank symbols on the tape. Each blank symbol is effectively an instance of the Concatenation operator. Characterizations of the Universal Turing Machine (UTM) has having "a finite" input is a lie or a least something worse -- a misleading or a confusion on the part of the theorist.
This implicit kind of "infinity" is the first of example of a "hiding." As mathematical systems get "more complicated," there will be other "infinities" and "zeros" (like implicit blank symbols) that will be uncovered and then covered again. These hidden infinities and zeros will make the invasion of randomness and order more complicated. The choice or "fabrication" of mathematics is intimately related to this hiding. Although Cantor was the first to explicitly introduce these kinds of fertile worms, and Russell was really the first to see them since Zeno and Heraclitus, the underlying worms in the rich soil of mathematics, not seen clearly by them and others. I try to expose them -- even though they are very hard to see: and they are slippery.
How do you build a computer? How about creating a digital circuit to produce the FUNCTION 10( )? The function 10( ), WHAT ARE YOU TALKIN' ABOUT!? Of, course, the function 10( ), the constant function 10. One does not need input for it to be a function. Now, you would think that the function 10 would be only one kind of function. But one can generate with different circuits different effects of 10, which for example I didn't specify what BASE the number 10 was in.... However, even with specifying 1010 the FUNCTION can be implemented as either boolean or two-complement or even clock pulses (counting ten beats). The point being memory (state) and time are entangled. And that is a problem, and a solution.
Toto, I don't think we are in Kansas anymore
when logic and proportion have fallen softly dead
Jefferson Airplane
In charactizing any model there is the model and its context. So for processes, the exchange of more empty polar time versus more full polar time is important to understand.
On the Monster Group:
The Monster Group is the largest finite exceptional Lie Group. The Monster has deep, complex FINITE symmetries. So the information contained in that Group, should tell us alot about replication and dissipation, construction and destruction, and all levels of finite complexity, since infinite groups cannot physically exist without infinite time. Time is nothing and everything, because it is a concept not a percept. The Monster Group includes (embedded) the information about important finite semigroups, finite quasigroups, important finite loops, and important finite monoids. We know about the contained "finite exceptional Lie subGroups" (19), but just as important we know the pariahs (6) exceptional Lie groups, which are NOT contained in the Monster as subgroups, just as some semigroups, quasigroups, loops, and monoids, may or may not be contained in the Monster . They are related, however. Relating and representing the exceptional (in and out) Lie groups, will provide insight into the different kinds of "time," "space," "energy," and "mass."
One can have a representation of something like "an algebra" or "God," and since a name or symbol has no meaning other what is inferred by the reader, the representations of that concept can be numerous as they are ambigious. For example, one could represent "god" as "dog" or "an algebra" as Monster Lie Algebra
A presentation of the Monster Group, the binary form of the order number:
100001101111101000111111010100010000011001000100111000010011111111011100010011000101011001110011110000100111110001111000110000110001010000000000000000000000000000000000000000000000
That's 180 binary digits, 113 zeros, 67 ones. 67 is the largest prime of the order of the Lyons group, which is one of the six pariahs (exceptional Lie groups not a subgroup of the monster).. And 67 is the third smallest irregular prime.
Another similar (in some sense, equivalent) presentation is: 246·320· 59·76· 112·133·17·19·23·29·31·41·47·59·71
Another way to present is: 2 · (23 · 320 )· (23 · 59 )· (23 · 76 )· (23 · 112 )· (23 · 133 )· (23 · 17 )· (23 · 19)· (23 · 23 )· (23 · 29)· (23 · 31)· (23 · 41)· (23 · 47)· (23 · 59)· (23 · 71)· 23
Yet another presentation is: 2 · (23 · 1 · 34 · 23 · 59· 34 · 23 · 76· 34 · 23 · 112 ·34 · 23 · 133· 34· 23) · 17· 23 · 19· 23 · 23· 23 · 29· 23 · 31· 23 · 41· 23 · 47· 23 · 59· 23 · 71· 23
There is some information that is NOT explicit about the properties of the Monster in this presentation. For example, the primes NOT part of order number of the Monster, include 37, 43, 53, 61, and 67. The primes in the Monster include only the primes that have a genus 0, not a genus of any other. The primes less than 71 not in the Monster: 37, 43, 53, 61, and 67 are genus 1.
But there all kinds of concepts that help in understanding the Monster: a few that might be interesting are specific generalizations of algebras; Magmas, Semigroups, Bands, Quasigroups, Quasivarieties, Loops, and Groups, not to mention Abelian Groups and Non-Abelian Groups. Lastly, Galois Groups versus Lie Groups or Galois/Lie Algebras.
Magmas
Quasigroups (quasivarieties quasiindentities ) vs Semigroups (bands )

Lattice of Bands
Loops vs Monoids( [ transition monoid and syntactic monoid ] vs [ trace monoids and history monoids ])
The Sporadic Groups
Lorentz Transform, courtesy of Wikipedia, CC-by-sa 2.5
Minkowski Space is characterized by a three dimension space and one time axis.
x2 + y2 + z2 -t2 = 0
The Monster is based on the Leech Lattice.
12 + 22 + 32 ... + 242-702=0=702- 12 - 22 - 32 ... - 242
Quantum mechanics, with its leap into statistics, has been a mere palliative for our ignorance -- Rene Thom
All mathematicians are liars
Anonymous
Make everything as simple as possible, but not simpler.
Albert Einstein
There is a natural list or an implicit "lattice" of "complification" of objects that increase the abstraction, concreteness, complexity, and simplicity of the list and the implicit lattice. How the lattice is interpreted (or viewed) changes the criteria of "complexity."

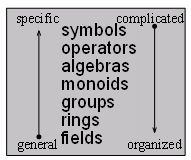
A string of symbols is the most "syntactic" and without meaning, in some sense "ordered." A natural system (part of reality) is the most "meaningful" and organized without syntax, and with little perceived order. A mathematical field is a specific example of a symbolic system that has a combination of syntax, meaning, and organization.
Level 0: Creation and Deletion |
Level 1: Unitary Operators |
Level 2: Binary Boolean Operators |
Level 3: Simple Arithmetic Operators |
Level 4: Replication/Dissipation Operators |
kEDM(n) = abs (int (log2 (n)) + infinity if 0 =/= (log2 (n))-int (log2(n))
It is true always that 0 = 0 + 0i + 0.00j + 0.k and 1 = 0i + 0.0j + 0k + 1. So what kind of nothing is zero? Is a not not nothing or just nothing?
Given matrix multiplication: what kind of zero is
Symmetric groups
The symmetry group S of an object is the group of all isometries under which it is invariant with composition as the operation. It is a subgroup of the isometry group of the space concerned. The spheres ![]() and
and ![]() to
to ![]() , and these maps generate the homotopy groups in those dimensions
, and these maps generate the homotopy groups in those dimensions
Rules are a part of a formal system. Given that any formal system can partially encode a natural system (or another formal system) by binary numbers, there will be some kind of encodings as following.
m1: 0 → 1, m2: 1 → 0
This is of great moment. These forms represent including a kind of infinity and zero.
There will be in essentially all formal systems a form of the following:
0 → 1 → 0 (and its dual 1 → 0 → 1)
This form is special. It is one of the simplest circular forms, and this is the basis for all other circles and more generally the basis for all self-reference. The various circular forms vary in their "size," "width," and "branches." For example, in the natural numbers (ala Peano axioms), the binary encoding of modulo 2, is one encoding this form. The ¬ NOT operator can often defined recursively, like ¬¬ X = X, essentially a self-reference form of a standard boolean logic.The understanding of how language "works" is often taken for granted. In mathematics, this is operationally true. Implicit in the formal system is the change in "state" from one time to another, and this includes the set of symbols in the formal system (the computer logic and memory (ROM or RAM) is analogous). In looking at formal systems for their use, the primary feature that is used is the entailment. Entailment works best if it is DETERMINISTIC (although it maybe not non-monotonic), and in reality this is the only kind of inferential entailment we are really interested in. For now we won't consider probablistic methods or reasoning.
Formal axiomatic systems are composed of several things: one explicit thing is its symbols. A set of symbols can serve differing roles. "Constants" are symbols that "stand for themselves." They represent a limited form of fixed point of "call by value." Variables serve as black holes, which can refer to anything, whether that be: call by value, call by reference, call by name, or call by result. However, the variables in mathematics most often refer to numbers. Conventional mathematics implies that the variable are of strong type, but whether they are, depends on the individual mathematical system, which typically consider functions as a form of (complicated) fixed point also. Symbols as function names can make the formal system usually infinitely complex, in general, however, there can be simple versions. Axioms of the formal system can be explicit or implicit, "most" being "explicit" -- however, there is a infinite number of implicit axioms.
You put your money in, and take your chances
Anonymous
There is no such thing as a free lunch.
Anonymous
Symbols can represent anything. Most often in mathematics and mathematical logic equations, the symbols are implicitly are of two kinds, variables and operators.
Functions are limited to representing numbers, although one can generalize to a set or matrix of numbers as in a matrix function. Equations are considered a comparison of two numbers, although the important part of the equation is the implicit set of numbers representing the solution of the equation. the solution can be a no points, one point, a set of points, a line, a surface, a manifold. What is not explicitly represented by a function is any dynamic process.
Let us consider the most basic form of mathematics in form of mapping
Y->f(x)
What is fixed is f. x represents an element of the SET X. Y represents the set of elements, named by y.
One can play a trick and write another mapping:
Y->x(f)
f(s)=s'(f)
Level 0: Creation and Deletion
» -> a, 0, 1
Level 1: Unitary Operators >0 -> 0
Level 2: Boolean Binary Operators
One of the simplest formal systems is what is called Junctional Logic. Based on the operator ^ (AND), Junctional logic is one of the simplest binary functional systems (in the form of a meet-semilattice of lattice theory).
0 ≡ 0^0,0^1,1^0 (3); 0^0^0, 0^0^1,0^1^1,1^0^0,1^1^0,1^0^1, 0^1^0 (7) ... (2**n)-1
1 ≡ 1^1 (1); 1^1^1 (1) ... n
Junctional logic is primarily dissipative. That is, information is forgotten, except when all input is one.
•“Simple Finite” Boolean Logic – ( Junctional, Equivalential, Implicational , Propositonal)
A more "complicated" system is Equivalential logic,•“Infinite Arithmetic” (+,-,*,/) Simple Groupoid, Fields, and Rings – N,Z*,Z,Q
Addition is a complicated operation when compared to the sixteen boolean operations. Addition preserves some of the state, when compared to the reductive binary boolean operators. The arithmetic operators (+,-,*,/) are in some sense "equilibrium operators" in the sense that they have inverse operators and the amount of "state" is in general is preserved.
What are the relationships between "normal," "orthonormal," "orthogonal," "perpendicular," "dependent," "independent," "degrees of freedom," and "asymptotic freedom."
By building "things" by a "simple" route, this does not imply that a "thing" is simple or complex in the same regard when looking at the "thing" once it is "built."
For example, consider that one constructs a "number" by the simplest method of Peano axioms. Take the numbers 6, 7, and 8. Now there are an infinite number of ways to build these numbers using all kinds of operators more complex than "successor", but let us look at the "simplest" and the "least number" of steps (in other words, using operators) and let us restrict it to simple binary operators, namely two (+,*)
6 (6+0,1+5,2+4,3+3,4+2,5+1,0+6; 2*3)
7 (7+0,6+1,5+2,4+3,3+4,5+2,1+5,0+7; prime)
8 (8+0,7+1,6+2,5+3,4+4,3+5,2+6,1+7,0+8; 2*4)
Obviously, the "complexity" of a number in respect to the operators +,* is different for each number. The complexity of a number in the sense of possible constructions is linear (function of n) for + and varies from 0 to x (non-linear function of n?) . The point being the complexity of one operator + increases montonically whereas the other operator * can be a form of "bottleneck" where "complexity" disappears (at primes), not a function of the "size" of the object only a relationship between ALL numbers before it. Complexity collapses. Thinking of complexity as a string (the natural numbers), the surrounding string "thickness" (much like a feather) from the complexity of the multiply operator, forms a simple two dimensional "topology" (in some sense of a "pretopology") with the metrics of complexity of + and *.
F[n,binary-complexity(+,n),binary-complexity(*,n)]
[(0,1,0),(1,1,0),(2,1,0),(3,1,0),(4,1,1),(5,1,0),(6,1,2),
a+b=c => log2(a)+log2(b)=log2(c)
a ^ b | a ⊕ b
triality
Dr. Euler's Fabulous Formula.
The Monster Group
•Equation Chaos (Q => R) [ A, T ]
•“Finite Commensurate Algebras” R,C,H,O (normed division algebras)
•Dimensional Chaos “Heaviside” (Euclidean) Topology: Tensors
•Infinite Incommensate Hypersurfaces (infinite dimension hypersphere => 0)
No, it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways.
Srinivasa Ramanujan
4.1 Representations -- Encoding: Operators and Types
All mathematical symbols (that represent types of things) are either constants, operators, or variables; however, in reality one can always extract operators (in the form of symbols) and represent those operators in conjunction with those variables, constants, and operators within formal systems. All symbols can be infinitely complicated, by continuely extracting operators. The classic example of this operator extraction is of adding zeroes or multiplying by ones (i.e., operator identities). In one hierarchy of types of numbers one can view the "complication" as addition of more and more complex operators, that is: substitution/elimination, unit concatenation/reduction operators, boolean (16 logic operators), finite modula concatenation (natural numbers: binary, octal, decimal, ... representations), integer (included minus or plus operator), rational (division operator), algebraic (linear recursive operators), transcendental (general recursive, computational operators), processes (continuous input and output).
4.2 Encoding and Decoding.
An irrational number cannot be expressed as a ratio of two integers. In otherwords, all irrationals cannot be encoded with integers with a simple, one time, finite set operation of division. Another way to say this is: one cannot decode all irrationals into integers without adding information that is not treated strictly as finite integers and/or one division operator. If one encodes a concept in a certain way within a formal system, and a contradiction can be proved, then the system is said to be vacuous as a "truth system."
The strategy in mathematics is to find statements (encodings or decodings) of either properties of an encoding or decoding of a particular entity, that being either a syntactic object within the formal system, syntactic object with referencing another syntactic object within the formal system, a syntactic object refering to both a syntactic object and a natural observable entity, or a syntactic object referencing a natural entity that is posited to exist.
The following story has a point; however, it takes about 35 years for closure on that story. There are three events that highlight the story.
I was proud and confident on my programming ability when I was young, since few kids had such experience with computers at that time. I had done a programming project in high school for my senior science project (1967). I wrote in three different computer languages, programs to solve "Instant Insanity." Being proud of that accomplishment, when my university professor (John Seely-Brown) was going to talk about Instant Insanity in his computer course, I piped up, I had solved the problem by computer, by brute force, trying most possible combinations (some I had pruned for the computer). John, responding to my comment, said in effect, that was a dumb way to solve the problem, one could have done it easily by using group theory, one did not have to use the brute force of trying all combinations, and checking for the correct result. Thanks John, I needed that. I, of course, swallowed my pride, and paid attention to what he had to say about groups and graphs, a very useful and powerful set of techniques in representing SOME kinds of information. Alas, I never offered my insights or unbridled thoughts to John, ever again. I did however, observe who he gave the benefit of the doubt or regard to in the following couple of years.
He was a great teacher and a very smart man, despite his lack of diplomatic intelligence at the time, so later I gained some very important insight from him in how people "think" and don't think.
John Seely Brown gave a very interesting talk later on about how kids did or did not learn, in particular, arithmetic. He had a AI program, as part of his research, called Buggy that figured out how kids did wrong (and implicitly right) in adding numbers. What he found was addition is a "complicated" procedure, and if you don't teach it right, some kids won't get it right, the first time. In fact, if you don't give them the right feedback, it is hard for them learn it, because you didn't teach them well enough and you don't understand it yourself well enough. Teachers not understanding what the kids did right and what the kids did wrong could not easily help the kids, other than giving simple feedback:, this problem you got right and you got this problem wrong. Pretty thin, feedback, I would have to say. However, letting the student figure out how he went wrong, and distinguish that from what he got right in all problems, is a harder for the teacher, in the short run, but better in the long run if the teacher is well versed in how students understand or don't understand.
For example, consider the following student's work. What is he doing right and what is he doing wrong? -- the hint is the student is doing only one thing wrong.
| 2 + 3 ___ 5 |
2 + 7 ___ 9 |
1 + 7 ___ 8 |
3 + 3 ___ 6 |
9 + 3 ___ 3 |
3 + 1 ___ 4 |
7 + 6 ___ 4 |
6 + 7 ___ 4 |
It should be obvious to you what the student has wrong and right, Thanks John. However, just in case you are dumb let me give you some more examples.
| 1 + 2 ___ 3 |
12 + 7 ___ 19 |
14 + 7 ___ 12 |
23 + 3 ___ 26 |
9 + 1 ___ 1 |
8 + 3 ___ 2 |
6 + 6 ___ 3 |
16 + 7 ___ 14 |
Ok, so the fact that the student doesn't have the right procedure to handle the carry digit, in this limited set of examples, even though he knows his addition tables below ten and adds the carry bit into the first radix position. But he really has no idea about magnitude (or/nor probably cares), that some numbers are bigger than others, which is a semantic notion. He is just going thru the procedure that he created, which is perfect legitimate because it gives him a result and it is logically consistent in his system of thinking. It just isn't what the teacher wants. His creative system works for him. But if you just tell him what problems he gets wrong and what problems he gets right, he still has to figure out what he did right and what he did wrong, in both his right and wrong answers. Most kids can do it, drill and kill, despite and because of their teacher and the school system. Most kids learn despite school, at least in the younger grades.
"The first principle is that you must not fool yourself-and you are the easiest person to fool. So you have to be very careful about that. After you've not fooled yourself, it's easy not to fool other scientists. You just have to be honest in a conventional way after that." -- Feynman
Well, of course, shame on the teacher and the school system if she/he does this. Thanks John. But WHAT IF THE TEACHER is the natural world, can you blame it for only telling you when you are right and wrong with the answer (that is, the result of "nature" computing-- reality -- like adding)? Nature's answers, sometimes on how it works, and why it works, are hidden from us. This is absolutely true beyond the Planck wall.
I kept my insight gained from John's insights, and my question to myself: hidden from others.
Fast forward, over thirty five years ... while reading the history of Quantum Theory... Paul Dirac had a theory (and a symbolic representation of that theory, i.e., mathematics) that is mathematically equivalent to Schrodinger's and Born-Jordan-Heisenberg notations. The problem was, Dirac's theory did not explain well the Lamb shift. Although physicists realized that quantum theory, as formulated in the 1930's, did not take into consideration relativistic factors (in other words, Einstein's new ideas about space and time). That was dumb, they knew something was missing.
Mathematically Dirac's formalism could accommodate relativistic factors, just not well. Semantically, old quantum mechanics has no explanation for relativistic factors.
How did they fix it? Well, they haven't completely --- but they (the new guys in Theoretical Physics in 40's and 50's: Feynman, Schwinger, Dyson, and Tomonaga) found better mathematical techniques and new objects. Their solutions and theories, called QED, are a combination of "semantics" (ideas about reality -- in particular physics) and "syntax" (ideas about symbols -- in particular mathematics). Later QCD was devised a refinement for the 60's and 70's. They also posited an "object" (read a semantic object)-- called a "graviton" -- a "particle" that might exist, which had no specific mathematical relation, to the Standard Model.
Currently in conventional theoretical physics, M-theory (a unification of string theories) are considered, by the scientific MOB, the "leading" edge of physics, but they are typically considering mostly physics as their "semantics" and "mathematics" as their syntax. What would prevent them from using the "semantics" of biology (or evolution) and the syntax of "information science?" Answer: they haven't been studied it and their interests (and their expertise) don't include those domains.
I don't think we are in Kansas anymore.
The Hamiltonian versus The Langrangianmass= equilibrium energy, energy not structure, input and output, C squared -- C input C output.
The map is not the territory, but neither is a random sample, but they are both starts. They are better than nothing or doG. And when they are combined intelligently, they are an unbeatable combination.
Keirsey's law revised.
"You can't beat first order statistics"-- the herd(strong correlation),
-- unless you know the first order correspondences too,
and you don't get in the way.

... was the right answer for me at the time. But in a crazy and 40 years from recall, the answer was luckily wrong.
No, it wasn't Yorick who answered. That's not right, he is dead? No, Yorick isn't dead, he is a fictional CHARACTER. Can fictional characters, die? Or when do they die?
There is no correlation there? What is the correspondence?
A rose is a rose is a rose is a rose, by any other name.
Well, ACTUALLY, it was Yorick. Yorick Wilkes -- The surface correspondence was in the first name. Correspondence versus Correlation. Correspondence and Correlation. Big difference, as my father would have said. But, he is dead. Dr. David Keirsey is dead. I am Dr. David Keirsey, and I am not lying. But I could be lying down at this moment you read this, nobody knows, you, me, my father, Yorick, Yorick, and doG.
Yorick Wilkes' answer, at the time, was a comment to me about the philosophical notion of "truth". He presented me with a similar gedanken situation as below.
Suppose, a friend who is not particularly aware of details, had a watch (the old kind) but he hadn't paid any attention to it (you know a crazy nerd like me). And this watch was broken -- it had stopped. You happen along and ask "What time is it?" Further suppose, it had been 2 o'clock, at the time, and he looked at his watch and said, "it's 2 o'clock"
Yorick proceeded to say essentially: The friend is saying the "truth" but he is not telling truth. There is a difference between saying the truth by coincidence and telling the truth for the "real" reason.
Ok, correlation is not causation. Check. Got it. On with life, PhD, family, and c/a/r/e/e/r.
But what was my question? Then and now. Well, actually, questions -- plural. The question is different from then and now. And the answer(s) are different too.
What are the RELATIONS between Correlation and Causation, and the RELATIONS between Correlation versus Causation -- besides NOT?
Yes, James Watson, you got it totally right and totally wrong. Now he is getting it crazily right and madly wrong. In Greek, it's called S c h i z o | p h r e n | i a, in plain old English is it called "all messed up".
Let us look closely at a two famous proofs: The Pythagorean theorem and Proof of existence of irrationality. These two proofs will serve to illustrate the issues of encoding and decoding.
Famously, the Pythagorean theorem is characterized in mathematics as a proof by construction. Another way to saying essentially the same thing is a proof by encoding. An important thing in this process is to realize - that a syntactic encoding of an syntactic encoding still looks like an syntactic encoding. Moreover, an syntactic decoding of a syntactic encoding looks like an syntactic encoding also, but we cannot tell the difference by the syntax of a particular language for they could be "equivalent", unless we know about the semantics.
The proof of existence of irrationality is also instructive for it is a proof by contradiction.
Language Encoding: Chasing Words
Most kids discover the ultimate futlity of "explanation" -- They will play a game by asking Why? for every explanation you give. And of course when trying to learn a new word, looking in a dictionary, everything is "defined" from other words.
The problem with word chasing is illustrated by a personal story about Richard Feynman.
Richard understood his father very early in his childhood. Melvin Feynman had not been able to pursue his own interest -- science -- because he never had the means to pay for advanced schooling. Luckily, his son naturally had the same temperament and interest, Melvin got his wish that his son became a scientist. Melvin and Richard were close, for they would take long walks and Melvin would talk to Richard about the world. What Melvin did was to teach his son to notice things.
'He ... taught me: "See that bird? Its a Spencer's warbler." (I knew he didn't know the real name.) "Well, in Italian it's Chutto Lapittitda. In Portuguese, it is Bom Da Peida. ... You can know the name of the bird in all the languages of the world, but when your finished, you'll know nothing whatsoever about the world. You'll know about the humans in different places, and what they call the bird. So let's look at the bird and see what it is doing -- that's what counts." I learned very early from my father the difference between knowing the name of something and knowing something.'
In the world of formal systems, the idea of canonical systems is popular (i.e., Turing machines, Real numbers, or predicate calculus). There is one major problem with these canonical systems -- there might be a set of formal equivalences for each "equivalent" in syntactic terms but this does not mean that they correspond to "semantic" equivalence. Model theory tries to address this problem of semantics by primarily two-valued logic, but only deals with "truth" and "false" or "in" and "out" -- typically semi-vacuous (or thinly abstract), binary landscape.
In mathematics you don't understand things. You just get used to them.
John Von Neumann
More than any other science, mathematics develops through a sequence of consecutive abstractions. A desire to avoid mistakes forces mathematicians to find and isolate the essence of problems and the entities considered. Carried to an extreme, this procedure justifies the well known joke that a mathematician is a scientist who knows neither what he is talking about nor whether whatever he is talking about exists or not. Elie Cartan
What is external symmetry versus internal symmetry? What is symmetry?
Alan Weinstein said in 1996:
Mathematicians tend to think of the notion of symmetry as being virtually synonymous with the theory of groups and their actions, perhaps largely because of the well known Erlanger program F. Klein and the related work of S. Lie, which virtually defined geometric structures by their groups automorphisms. ... In fact, though groups are indeed sufficient to characterize homogenous structures, there are plenty of objects which exhibit what we clearly recognize as symmetry, but which admit few or no nontrival automorphisms.
The important thing to notice, which is subtle if not obscure, is the phrase "no nontrival automorphisms" -- in other words, from this phrase it must be inferred that an automorphism (trival at least) is a necessary part of symmetry. Of course, this should be obvious, not surprising, but like all important foundational ideas, it is crucial in understanding the underlying semantics of symmetry. Understanding the notion of an inverse is central to understanding and defining symmetry. The problem comes in WHAT IS AN INVERSE? There is ambiguity here. Both locally and globally, continuous and discrete.
reflection symmetry, continuous symmetry, group symmetry, self-similar symmetry
Questions about the nature of the self has abounded since at least the time of antiquity ... Lonnie Athens, The Self as Soliloquy.
Of course, Athens is implicitly refering to the "human" self, but the statement is also true of the general "self" or the "abstract" notion of "self."
two-bit: adjective, slang: mediocre, inferior, or insignificant
I have a two-bit theory that explains everything in the universe. It's my theory of everything. I call it the "dog" theory of the universe. True, it is a abstract theory, but all theories are abstract. All of them have to use words (or symbols) that refer to the natural world. The two bits are: Dog=1; not Dog=0.
So why do we exist? Answer: "dog." What is our purpose? Answer: "dog." What is evil? Answer: not "dog." (or "god").
You get my drift... For those who need more...
I have a two-bit formal model. One might call it: Propositional Logic. Statement is either in the language or not, and if it is in the language it either it is True=1 or it is False=0.
Actually, this two-bit formal model is more than two bit, since the propositions can be of any length, and the grammar of Propositional Logic is a tad bit more complicated, all though one can use Sheffer's stoke which is pretty simple. But the point is, a model that has only "two" values, True or False, it is a pretty vacuous way to represent the world.
You get my drift... For those who need more...
One might consider a theory with an infinite set of bits to be "more complicated" than a two-bit theory, but in reality, infinity is typically a simple case in mathematics -- its 3, 4, 5, for example, when "things get" complicated. Again, diophantine equations are hard, whereas the real number line covers a multitude of sins. But of course, I am not advocating that we abandon the problematic notion of infinity. But we can't be all, lucky, and brilliantly naive, as Euler.
Where is there is structure there is at least one function;
with no structure, there is no function.
With no function, there is no structure;
where there is function there is an associated structure.
But structure is not function and function is not structure.
Structure and function are Keirsey-Hegelian complements.
It is has been said previously, the generic notion of "function" (which is closely related to "purpose") needs to be formalized and analyzed to a larger extent.
The problem is, of course, where does one start?
Since "function" by its very nature is abstract, it is necessarily both arbitrary and ambiguous. Its nature is very much like language, except language can be meaningless, whereas function is closer to semantics. Structures (real objects) are meaningful; human written structures (language constructs, e.g., equations, words, strings) can be viewed as meaningless but have at least one function (existence).
Constructing functions by constructing formal structures in multi-language framework (and the associated "action corpus"), and then infering functions by "functional computation" is the point of this exercise.
One approach is to start from the "bottom up," the other is "top down," but ultimately evolutionary dynamics in combination is the approach that must be employed.
What is the nature of noun phrase in English?
Red Fox, Blue Fox, Running Fox, Slow Fox, a Dead Fox, a plastic Fox, a non-Foxy Fox.
Green Ideas Sleep Furiously.
x-like y
The Time Has Come To Speak Of Many Things
The Walrus
Let's take a specific example. Which unfortunately, or fortunately, is not very specific.
"Time-like space." What does that mean? Actually, the better question is what could it mean? It could mean many things. The time has come to speak of many things, but not too many things. How about just "two many" things. How about Sqrt(2) and 2.00002 ? Euclidean Space is "SPACE-like" whereas the Minkowski space - is TIME-like. But what is "TIME" and what is "SPACE"?
Poincare group is ergodic. But the universe is always changing (almost) -- what do we mean by changing? There seems to be some order in universe, so maybe it isn't changing ALL the TIME. Maybe just SOME of the TIME, or maybe SOME of the universe? What SOME? Maybe the SOMA (the old word for "body"), or in other words, "mass" -- but what is mass, but dynamic energy -- dynamic energy? What are you talkin' about? Energy in dynamic equilibrium? So what is this "thing" dark matter? And what is its relationship to this "thing" called dark energy?
F<S>

A complicated and abstract mathematical notion is the groupoid. The groupoid G can defined as having a base set B and a set G which can include B. The set G are composed of isomorphisms such all elements g in G have an inverse.

It's just a fixed point.
John von Neumann's response when as a graduate student, John Nash, presented Nash's equilibrium ideas to von Neumann.
We can't solve problems by using the same kind of thinking we used when we created them.
Albert Einstein
Ich war so drumm als ich jung war.
(I was dumb when I was young)
Wolfgang Pauli
As far as the laws of mathematics refer to reality, they are not certain, and as far as they are certain, they do not refer to reality.
Albert Einstein
First, most mathematicians consider Nash's embedding theorem, rather than the Nash equilibrium, as his important work, in mathematics. The embedding theorem was considered counter-intuitive at the time, and his proof of the theorem was considered genius.
In the case of Nash's equilibrium, his PhD thesis, he had an appointment with Von Neumann, before he had completed the work. At the time, Von Neumann was like a god, and Nash, a lowly grad student, nervously and humbly started to explain his ideas, and Von Neumann, reportedly cut him off. Gruffly, and dismissively, remarked --- it's just a fixed point. Technically, Von Neumann was right. But there is that pesky hammer word JUST.
In reality, Nash's equilibrium is more of an application of mathematics, rather than "pure mathematics." In some sense, Von Neumann's work on game theory is very weak, because it's too limited in applicably. Bluntly, one could say Von Neumann's game theory work is JUST mathematics, it rarely can be applied to the "real world". Whereas Nash's work was more applicable to modelling reality (hence more useful). [But even Nash's equilibrium is rarely true either, but it was a vast improvement and advancement, at the time, over Von Neumann's work.]
How can you understand something about life without understanding something about non-life?
This is a question I put to my father. And of course, there is the equally important problem of how can you understand something about non-life without understanding something about life. This latter problem was something I tended to ignore, when I was younger, before I realized that my father (in area of systems-field theory) and biology had some important lessons to be learned by the likes of me, Physicists, mathematicians, and other "hard" science types-- that is, all unknowning or knowing precise, but abstract reductionists.
How do ideas originate?
One point of studying history is that it gives you an indication of what's likely to happen now, if you can find an appropriate analog in the past. This is a tricky business because as you look at factors contributing to a trend, it's not easy to determine which ones are really important. Making that determination is a judgment call, and everyone's judgment is colored by his worldview, or Weltanschauung as the Germans would have it. Doug Casey
In 1900, Max Planck had created a theoretical explanation of Wien's formula on black body radiation. But in that process, experimentalists aware of Planck's interest in the matter, had recently looked into the matter at longer wavelengths and higher temperatures, and told Planck that the infrared region at high energies violated Wien's formula -- so his original explanation was wrong. To quickly solve the problem, Planck added a "correction" to his analysis. A resulting derived formula proved to correct, no matter the increase in frequency (looking at a wider range of energies) and the improved accuracy of experimental results. Planck went back to his quickly modified analysis and reformulated his ideas to justify the semi-ad-hoc correction and found that it implied that energy was emitted or absorped in discrete units based on Boltzmann's combinatorics. He had solved a problem by simply creating a "chimera:" adding a factor in his equation -- but he did not realize its consequent was as significant until he tried to justify his change theoretically. Even then, he did not consider it as profound, until Niels Bohr and others started to apply his new idea "a quantum action" to atoms and molecules. Another problem was there was a flaw in Planck's reasoning for which Satyendra Bose corrected later, but the idea of quantum action has proved to be one of the two key and major ideas of physics in the 20th century.
Niels Bohr became very successful in applying Planck's quantum action idea when examining the spectrum of the hydrogen atom. The failure of Rutherford's simple analog "orbit" model, whereas the precise predictions of Bohr using Fraunhofer spectral lines, signaled the death of 19th century physics in the realm of small. However, for more complicated atoms, Bohr's model wasn't as accurate, so his original ideas needed modification or to be added to.
Ersatz
Involution and Envolution of Ideas
New Data: Sommerfeld, Bohr
What is a Quantum, what is irreductible?
Curie point, phase transition
Heisenberg did not know about matrix multiplication.
Max Born
Johannes Kepler was a Protestant in the sixteenth century. In 1589, after moving through grammar school, Latin school, and lower and higher seminary in the Württemberg state run Protestant education system, Kepler began attending the University of Tübingen as a theology student. For brevity I include a paragraph from Wikipedia.
Johannes Kepler's first major astronomical work, Mysterium Cosmographicum (The Cosmographic Mystery), was the first published defense of the Copernican system. Kepler claimed to have had an epiphany on July 19, 1595, while teaching in Graz, demonstrating the periodic conjunction of Saturn and Jupiter in the zodiac; he realized that regular polygons bound one inscribed and one circumscribed circle at definite ratios, which, he reasoned, might be the geometrical basis of the universe. After failing to find a unique arrangement of polygons that fit known astronomical observations (even with extra planets added to the system), Kepler began experimenting with 3-dimensional polyhedra. He found that each of the five Platonic solids could be uniquely inscribed and circumscribed by spherical orbs; nesting these solids, each encased in a sphere, within one another would produce six layers, corresponding to the six known planets—Mercury, Venus, Earth, Mars, Jupiter, and Saturn. By ordering the solids correctly—octahedron, icosahedron, dodecahedron, tetrahedron, cube ...
However, Kepler much later very reluctantly rejected this model, because it didn't work. Moreover, he rejected the current and available data, knowing it's inaccuracy. Needing more accurate and numerous measurements thinking that those would prove his theory, he came in the employ of Tycho Brahe, inheriting the data, when Brahe died. But the data did not fit. Abandoning his "perfect" idea using the symmetric and simply described platonic solids, he followed the data. After painstaking analysis and a great deal of effort, Kepler working with data realized that data pointed to elliptical orbits. Changing his model to ellipse, he matched the data perfectly. The original general "idea" -- applying mathematics to physical processes, was right, whereas his specific and initial mathematical model (guess) which suggested a specific regular pattern did not correspond to the pattern he ultimately observed, and hence he was wrong initially. On the otherhand, an ellipse is very accurate model of a planet orbit, but still an approximation, since the multi-planet (many body problem), is ultimately not solvable, hence not predictable.
New Math: Heisenberg, Born, Dirac, Schrödinger
Schrodinger developed wave mechanics, which initially was shown to be mathematically equivalent in Heisenberg-Jordan-Born matrix multiplication.
Lanczos pointed out in his paper the ' closest connection ' (' engsten Zusammenhang ') that existed between the matrix mechanics of Heisenberg , Born and Jordan and the theory of integral equations . He stated in particular : ' The equations of motion and also the quantum condition can be written down in the form of integral equations. Thus a continuum interpretation arises, which has to be compared to the discontinuum interpretation [ of Born , Heisenberg and Jordan ] as having equal rights, since there exists a unique relation between the two ' ( Lanczos, 1926a , p. 812 ). He further claimed : ' As far as the fundamental interpretation of the theory is concerned, the formulation in terms of integral equations possesses the advantage of being in immediate harmony with the usual field-like conceptions of physics ' (Lanczos, 1926a , p. 812).
Jagdish Mehra, Helmut Rechenberg. The Historical Development of Quantum Theory. (Springer, 2000). Page 643.
The matrix a must then be regarded as a complete representation of the function f(s, σ), since for a given [ set of elements ] a[i,k] the function f(s, σ) may be established in the sense of the formula [( 126 )]. On the other hand , the function f(s, σ) can also be considered as a representation of the matrix a, since one can immediately obtain from it, by integration according to the formula
the elements of the matrix. (Lanczos, 1926a, p. 813)
Jagdish Mehra, Helmut Rechenberg. The Historical Development of Quantum Theory, Vol 5, Part 2. (Springer, 2000). Page 644.
The point not to be missed --- Schrodinger versus Heisenberg -- assumes that continuity and discreteness are EQUIVALENT
Eigenfunctions can be represent a vector, matrices can represent points in a vector space. The wave function is considered a probability density function. A probability density is not a real thing. However, waves are a physical model: a semantic model.
Both Schrödinger and Born, Hesenberg, and Jordan methods had problems with
Quasi-dimension
Schwinger, Feynman, Weyl, Gell-mann
How do ideas evolve?
Dimension: Euclid, Lobachevsky, Gauss
Words! Words! Words! I’m so sick of words! I get words all day through;
First from him, now from you! Is that all you blighters can do?
Liza Doolittle
This sentence is not true.
A Truthful Liar
Wir mussen wissen, wir wollen wissen (We must know, we will know)
David Hilbert
Never express yourself more clearly than you think.
Neils Bohr
The remarkable thing is understanding never stays put. It is important always to get a new understanding ... ... ... understanding can be improved
Saunders MacLane
I suffer very. I English poor.
Michiko Hamatsu
Soon after coming back to America from Japan to attend graduate school, I received a letter from a Japanese student (who I had "taught" some English as a part of an English club). Her knowledge of English syntax was minimal to say the least. The remarkable thing about the letter was that I understood what she was saying. The above quote is part of that letter. Knowing some of Japanese grammar, the meaning was clear. She was saying: "I feel bad because my English is poor." Using the semantics and the context, there was no ambiguity, despite the ungrammaticality of her utterance. Grammar often has little semantic content: it often includes redundant information.
At the other edge of the spectrum, a canonical example in linguistics (circa 1980) was to show that a sentence can be "grammatically correct" but have no meaning. The example used was the sentence: "Green ideas sleep furiously." Being in Natural Language Processing, we had some disagreements with linguists, and we found their "example" as stupid. One could "create meaning" to make the sentence "meaningful." When I told this to my father (who was not familar with strum und drang of the linguistics field) this sentence, he also classified the sentence as "nonsense." But I then came up with a simple intrepretation of that sentence which did make sense. (Something like "new and immature ideas are in the minds of inventors are that churning around and eagerly trying to get out") he conceded that "meaning" was relative to the speaker(encoder) and the hearer(decoder) -- and their meanings don't have to have anything in common -- although typically does if you want communication (or miscommunication) to happen.
Another time I was talking to a fellow employee at the Hughes Research Labs, a chemist, and I announced that I was recent engaged to someone from Thailand. She said "Oh, I have some friends from Taiwan, they are very nice people." Of course, I didn't say anything to embarrass her in her ignorance, but I did realize that MY understanding of the word THAILAND as opposed to hers, was significantly different. Understanding that all of us are subject to this kind of ignorance came home to me when I was on the opposite end of a similar embarrassing moment. When talking to a person sitting next to me at international conference in the early 90s, despite my pride of knowing a vast amount of geography and history, when he said he was from Slovenia (newly formed), I proceeded to later in the conversation, to refer to his country as Slovakia --- oops -- a slip of the tougue. He quickly took umbrage -- I, was embarrassed of course, realized how major this faux pas was too. I knew there was a significant difference between Slovenia and Slovakia at the time (ethnicity being a touchy subject -- Germanic versus Slavic in flavor). The break up of the Soviet empire and influence created an alphabet soup of countries, for me to get confused about. His experience with the word "Slovenia" and the actual territory referred to by that word was much more signficant than mine, just as my experience with the word "Thailand" and the territory and its people was vastly superior to my chemist friend.
How can that mushy thing call "semantics" or "meaning" have anything to do with mathematics proper? Some mathematicians would like ignore meaning as much as possible: they are not interested in mathematics application to reality. On the other hand, the three giants of Mathematics: Archimedes, Newton, and Gauss are to a large degree more "physical mathematicians" than pure mathematicians like Hilbert, Godel, and Cantor. Moreover, theoretical physicist Andrew Witten has been able to develop some interesting mathematics in his pursuit of a model of strings and the universe. And, of course, Newton developed calculus in his pursuit of a model of the heavens. Nevertheless, some scientists find mathematics not very useful in their research: many biologists are the most notable in the group. Clearly effective use of mathematics in reality is desirable. But, how can semantics be incorporated systematically and systemically into mathematics, rather than the limited and ad hoc evolution that characterizes it today?
The excessive formalization of the Bourbaki group was opposed (or at least balanced) by Coxeter for a good reason. The failure to eliminate "semantics" has been established. Going in the other direction: incorporation of semantics as a science or even a mathematics must be the next envolution. Unfortunately, most mathematicians, if not all, would say: impossible. It must be an art -- and we must continue to say any semantics must be part of science, not mathematics. In all probability, Physicists and other scientists believe creating science is an art also.
I say no. I say, let us try to make mathematics more of a science (or at least more systematic and more understandable -- rather that implicitly obscure -- bordering on mystical and alchemical like those of the Bourbaki group or the random problem solving of Erdos), and make the making of science more of a science too. The creation of Mathematics and Science as ART all though organically the way they have developed, does not mean as they develop in the future, that they must continue to be in the dark ages. Of course, the skeptics will say -- how?
My answer, at the moment, is: with difficulty. On the otherhand, I see a glimmer of a path. The path is incorporating semantics with syntax systematically.
Thesis, Antithesis, and Synthesis: --- and AntiSynthesis (no, not no, no not, no no)
zero, infinity
zero,one,infinity
order-disorder
order-equilibrium-disorder
The two canonical or "typical" single dimensions in mathematics is Z, the integers and the "reals" R. More exotic mathematical "dimensions" are numerous. How can we build mathematics to have some meaning -- maybe talk about dimensions in meaning? --- In reality, we can't avoid semantics in mathematics. Hilbert was wrong. Rosen asserts:
The celebrated Incompleteness Theorem of Godel effectively demolished the formalist program. Basically, he showed that, no matter how one tries to formalize a particular part of mathematics (Number Theory, perhaps the inmost heart of mathematics itself), syntactic truth in the formalization does not coincide with (is narrower than) the set of truths about numbers.
... For our purposes, we may regard it as follows: one cannot forget that Number Theory is about numbers. The fact that Number Theory is about numbers is essential, because there are percepts or qualities (theorems) pertaining to number that cannot be expressed in terms of a given, preassigned set of purely synactic entailments. Stated contrapositively: no finite set of numerical qualities, taken as syntactical basis for Number Theory, exhausts the set of all numerical qualities. There is always a purely semantic residue, that cannot be acommodated by that syntactical scheme.
Euclid tried to encode his semantic notion of "space" into mathematics via the postulates of geometry and succeeded masterfully, until Bolyai and Lobachevsky and little later Riemann and finally Gregorio Ricci-Curbastro, illustrated that there was some natural ambiguity in Euclid's "concept" of space. In fact, it was Ricci and Levi-Civita who established the beginnings of tensors. The most recent proof of Poincare's Conjecture (now a "theorem") uses notions of "heat flow" in the form of adjoint heat flow equations (e.g., building on Richard Hamilton's Ricci flow). Using physical concepts to do mathematics has been done since Zeno, but what has not happened is trying to a systematic approach.
So, the real issue is how do we systematically incorporate "meaning" (or reality) into mathematics. String theorists and physicists in general have been trying to incorporate "basic" concepts such as "space," "time," and even "energy" and "mass," as a part of reality and the jury is still out in how successful they will be. They have been to some degree successful in blurring the distinction between mathematics and reality. On the other hand, the physicists have been somewhat driven by ad hoc, incremental ways. Brian Greene, an eloquent spokesman for string theory, has posited that at the beginning of our universe that things where "highly ordered." And the world now is in a state of relative disorder compared to the beginning, and getting more disordered: implicitly in "disorganization." String theory, in making this assumption, without both a scientific basis or a epistemological basis implicitly assumes that mathematics is physics. To quote Robert Rosen: [Life Itself, 5E On the Strategy of Relational Modeling, p117]
As we saw in the preceding section [Rosen's explanation of physics view of organization], the word "organization" has been synonymized with such things as "heterogeneity" and "disequilibrium" and ultimately tied to improbability and nonrandomness. These usages claim to effectively syntacticize the concept of organization but at the cost of stripping it of most of its real content.
Indeed, when we use the term "organization" in natural language, we do not usually mean "heterogeneous," or "nonrandom," or "improbable." Such words are compatible with our normal usage perhaps but only as weak collateral attributes. This is indeed precisely why the physical concept of organization, as I have described above, has been so unhelpful; it amounts to creating an equivocation to replace "organization" by these syntactic collaterals. The interchange of these two usages is not at all a matter of replacing a vague and intuitive notion by an exact, sharply defined syntactic equivalent; it is a mistake.
Let us look at what John von Neumann said again.
By axiomatizing automata in this manner, one has thrown half of the problem out the window, and it may be the more important half.
John Von Neumann
Von Neumann tried to produce a "self-reproducing" automata. Did he succeed?
According to Von Neumann and Arthur Burks, essentially Von Neumann had the right idea, if not actually completing a working specification. However, what is meant by a "self-reproducing" automata? What is "self?" What is "reproducing?" Is "self" 'a description of "self,"' or is self 'a description of a description of a description of... of "self."' Self cannot refer to Self with out making a paradox (or a impredicativity).
yes, BUT, it's more complicated.
my standard response to my father
Marx was right, he just got the wrong species.
E. O. Wilson
Give me a fruitful error any time, full of seeds, bursting with its own corrections. You can keep your sterile truth for yourself.
Vilfredo Pareto
1 -> 10
1 -> 1
1 -> 0
1 ->
1 -> a
All operations are replicative and dissipative. Inference is discrete. Computation can be continuous or discrete, but typically and implicitly is referred to, or thought as, digital and hence, discrete.
John Baez helps in giving an set of analogies in constructing finite simple groups. The details are complex; however, these specific analogies can give hints when applying analogous analogies to simpler (but more abstract, hence complex) constructs. I quote from John's This Week in Mathematical Physics week 263
One reason finite simple groups are important is that every finite group can be built up in stages, where the group at each stage mod the group at the previous stage is a finite simple group. So, the finite simple groups are like the "prime numbers" or "atoms" of finite group theory.
The first analogy is nice because abelian finite simple groups practically are prime numbers. More precisely, every abelian finite simple group is Z/p, the group of integers mod p, for some prime p. So, building a finite group from simple groups is a grand generalization of factoring a natural number into primes.
However, the second analogy is nice because just as you can build different molecules with the same collection of atoms, you can build different finite groups from the same finite simple groups.
I actually find a third analogy helpful. As I hinted, for any finite group we can find an increasing sequence of subgroups, starting with the trivial group and working on up to the whole group, such that each subgroup mod the previous one is a finite simple group. So, we're building our group as a "layer-cake" with these finite simple groups as "layers".
But: knowing the layers is not enough: each time we put on the next layer, we also need some "frosting" or "jam" to stick it on! Depending on what kind of frosting we use, we can get different cakes!
To complicate the analogy, stacking the layers in different orders can sometimes give the same cake. This is reminiscent of how multiplying prime numbers in different orders gives the same answer. But, unlike multiplying primes, we can't always build our layer cake in any order we like.
Let us look at a simpler construction and destruction (or more properly a reduction), where we look closer at the "cakes," "layers" and "frosting" than John does. Baez emphasizes the construction, but does not talk about the "destruction." When adding (or multiplying) numbers or groups, implicitly there is "reduction" (e.g., the making of a same cake in a different order). In the simpler case we will look at different operators as different frostings.
Let us look at a standard finite ring of integers (+,*), mod 64.
For example, consider the number 32. How does one construct it (compute it). Following is two "ways" of construction.
011111b + 000001b -> 100000b [6,6 bits + ~48 operations => 6 bits] {6*2 xor, 6*3 and, 6*3 or}
100000b * 000001b -> [0000000]100000b [6,6 bits + ~232 operations => 12 bits => 6 bits} {6*6 and, 23 xor, 128 and, 64 or}
(+ n-bits -> ~4n operations, * n-bits -> Cn2 operations)
So we can see that addition (+) is a composition of at least two operators (and & xor) and essentially linear in the number of operators based the size of the integer magnitude. Multiplication is a composition of at least three operators (and, +, shift) or a slew of ands, xors, ors; and essentially the number of operators based on the square of the size of the integer magnitude (actually if one is clever nlogn is the complexity, by reusing computations or multiple routing of same intermediate results). John Baez continues in describing the different layer cakes construction for simple finite groups.
Suppose we want to build a group out of just two layers, where each layer is the group of integers mod 3, otherwise known as Z/3. There are two ways to do this. One gives Z/3 ⊕ Z/3, the group of pairs of integers mod 3. The other gives Z/9, the group of integers mod 9.
We can think of Z/3 ⊕ Z/3 as consisting of pairs of digits 0,1,2 where we add each digit separately mod 3. For example:
01 + 02 = 00
12 + 11 = 20
11 + 20 = 01We can think of Z/9 as consisting of pairs of digits 0,1,2 where we add each digit mod 3, but then carry a 1 from the 1's place to the 10's place when the sum of the digits in the 1's place exceeds 2 - just like you'd do when adding in base 3. I hope you remember your early math teachers saying "don't forget to carry a 1!" It's like that. For example:
01 + 02 = 10
12 + 11 = 00
11 + 20 = 01So, the "frosting" or "jam" that we use to stick our two copies of Z/3 together is the way we carry some information from one to the other when adding! If we do it trivially, not carrying at all, we get Z/3 ⊕ Z/3. If we do it in a more interesting way we get Z/9.
In fact, this how it always works when we build a layer cake of groups. The frosting at each stage tells us how to "carry" when we add. Suppose at some stage we've got some group G. Then we want to stick on another layer, some group H. An element of the resulting bigger group is just a pair (g,h). But we add these pairs like this:
(g,h) + (g',h') = (g + g' + c(h,h'), h + h')
where
c: H × H → G
tells us how to "carry" from the "H place" to the "G place" when we add. So, information percolates down when we add two guys in the new top layer of our group.
Of course, not any function c will give us a group: we need the group laws to hold, like the associative law. To make these hold, the function c needs to satisfy some equations. If it does, we call it a "2-cocycle".
For the simpler systems, like the finite ring of (+,*), one "group" is the lower place (h) and the higher place is other "group" (g) the plus operator is as follow:
| + | 0 | 1 |
|---|---|---|
| 0 | 0 |
1 |
| 1 | 1 |
g1,h0 |
| h |
|
c |
|
(g,h) + (g',h') = (g ⊕ g' + c(h,h'), h ⊕ h')
The layers are the same, but in multiplication the frosting is different.
| * | 0 | 1 |
|---|---|---|
| 0 | 0 |
0 |
| 1 | 0 |
g0,h1 |
| h |
|
c |
|
d |
|
(g,h) * (g',h') = (g ^ g' + c(h,h') +d(h,h'), h ^ h')
Since the "cake" (a specific integer) is the same from building "layers" with "frosting," the molecule "cake" composed discrete elements (for example, 1, primes, and integers and operators). Specific examples 5+1=4+2=3+3=2*3=1*6=6 (101b+1b=100b+10b=11b+11b=10b*11b=1b*110b=110b)
Now, it is clear that addition and multiplication do not obey group laws as illustrated by Baez (again if one assumes modulo 2). But the "layers" and "frosting" in rings have an analogous approach to finite group construction. And, there other constructs besides finite rings, finite fields, etc. There are numerous kinds of "carrying" from one place to another place such that it can be "arbitrary." Different "laws" could be used; "symmetric," "abelian," "associative," "information preserving," "type perserving," "type destroying," "replicative," "dissipative."
Continuous manifolds (because of the real number infinities)in the combining of primafolds (3D closed oriented prime manifolds) are an interesting analogy in the higher Euclidean embeddings and spaces. In particular, it should be noted that for closed and oriented manifolds the Betti number for the k-dimension, is equal to the Betti number for the n-k dimension (where n is the maximum dimension of the manifold).
Replication -> Equilibrium (automorphism)
Dissipation -> Equilibrium (automorphism?)
Replication -> Growth (irrational, more state)
Replication -> Growth (rational, same state)
Dissipation -> Decay (irrational, less state)
Dissipation -> Decay( rational, same state)
Context Replication (birth), Dissipation (death)
Inferential closure. (discrete vs continuous)
inference paths. inference loops.
Lie Groups
rings
finite fields
Memory closure
Lie Algebras
linearity
Ideals
Simple Lie Groups revisited
Memory closure. (discrete and continuous)
Primafolds, number paths, computational paths, memory loops
Lie Groups
Lie Algebras
Prime Ideals
Exceptional Lie Groups
Monster Group
In "in" form "configurational shape" ation "situation"
Modern venucular (argot): coded bits, bytes, and data -- "what them computers mess with."
Take the concept of "layers of information" -- what does that mean? What does that "define?!" Well, the phrase "layers of information" does not define anything precisely but as we have discussed nothing (whether that be numbers and equations or words or phrases and sentences) defines anything precisely. It is a matter of degree and perspective or motivation. What could "layers of information" mean or what does it "define" imprecisely. Those who are familar with Internet protocols will not have a problem in having a good feel for what is meant here -- the TCP/IP protocols are considered one of the "lower layers" of information on the Internet that Hypertext protocols, a "higher level layer" are encoded as programs and files that operate on (or "on top of") the lower level "layers" of information. The "metaphor" or "analogy" (levels of information) works pretty well in this limited (but broad context). But, what of "things" of bosons and fermions, atoms and molecules (which "compose" practically everything) -- and for that matter the surrounding context of the "universe" -- how does this metaphor or analogy apply -- or does apply it at all? For those who find no use or no interest in this somewhat "well defined" or at least "described" metaphor, but metaphor nonetheless, should not read any more, otherwise, let's plow on.
Ex "out" form "configurational shape" ation "action, state, or process "
Modern venucular: a neo-logism -- the surrounding context "information" connected to the implied object's information.
Robert Rosen has a whole chapter on different uses of the concept of time [Anticipatory System, Chapter 4, Encodings of Time]. In particular he discusses: 1) Time in Newton Dynamics, 2) Time in Thermodynamics and Statistical Analysis, 3) Probabilistic Time, 4) Time in General Dynamical Systems, 5) Time and Sequence: Logical Aspects of Time, 6) Similarity and Time, 7) Time and Age.
So I would submit, time needs to be examined in context. Einstein did a detailed gedanken experiment with "light" and "time" but he did not examine closely the concept of "an event." What is "an event" -- this concept needs to be looked from an "information theoretic" perspective. Current theories fail to account for life (the complex) and quantum mechanics (the small) suggests there needs to be another gedanken experiment.
In physics: mass, energy, space, and time are treated as measures, which are related, but "space" and "time" are concepts whereas "mass" and "energy" are percepts. In other words, space and time do not physically exist (nor does spacetime, e.g., 3 + 1, exist either as simple construct), whereas mass and energy do physically exist. Now, having only one dimension of time, is mathematically and conceptually simple, but it maybe no longer be productive to have that simple of an encoding. It is time to consider "multiple dimensions of time." But before that one must examine the nature of reality, reference, inference, and reasoning.
The Evolution of Ideas
Let's look at something that conventional physics has said -- energy and mass are related. Of course, Einstein has found a "law" that seems to apply to most of the current Universe. But we know that if there was a "big bang" that his "law," E=mc2, does not apply "at the beginning" -- So what gives? Let us do a simple gedanken experiment on the Universe.
Consider the equation E/c=mc. This is just a rewrite of Einstein's equation.
First let's unpack this equation. c is the speed of light, assumed to be a constant by Einstein. Since it, c, is a constant, let us assume a different amount of information that involves that "constant." For example, consider a "precise" constant like e, Euler's number. Euler's number has, given enough time, -- an infinite amount of time -- it contains (or generates) an infinite amount of information. So what if we decide to represent c as a constant with an infinite amount of information? Now c as a constant has units associated with it: c = D/T, that is distance over time. So let us rewrite the equation again. E/(D/T)=m*(D/T)
So if those who like real numbers (that can represent an infinite amount of information) might stick in a real number constant. Let us chose our units so for energy E = 1, and mass m = 1. (That is we will count the Energy of the Universe = 1, and the Mass of Universe = 1, and the time of the universe as 1. So let's rewrite the equation, using these unit choices. 1/(D/1)=1*(D/1).
Simplifying. 1/D=D. Of course this "doesn't seem to make sense." (unless you use D=1) -- Maybe this demonstrates the Universe does exist. However, what does it mean from an informational point of view. If I use a "infinite information constant," is there any 'choice" that does make some sense? How about the "constant" ∞? So 1/∞ = ∞/1. You jest -- most people would say. But could you physically tell the difference between 1/∞ and ∞/1? Both require explicitly an infinite amount of information -- like 0 does implicitly. (Yeah, you have to think about that for awhile -- there are no short cuts in imagining this idea).
So you if you look from an informational point of view, 1/∞ ≡ ∞/1.
Thus the INTERNAL UNIVERSE (?multiverse?) ≡ EXTERNAL UNIVERSE (?our universe?). Hyperbolic-Space (?quantum world?) is homeomorphic to the Euclidean-Space (?our world?). Is Poincaire's conjecture, now a theorem, make our Universe possible?
The next question is what are the relations between the small (quantum world) and the large (our universe) -- string theory and such, model these relation syntactically by making up equations by ad-hoc, and historical intuition, but what about systematic semantics?
kTime the limit 0 ≡ 000.00002∞, kSpace the limit 1 ≡ 0000.111112∞, kEnergy the limit 2 ≡ 00001.1111111112∞, kMass the limit 3 ≡ 00000010.111111111112∞
Let us form a quasi-space of strictly time.
The Dialectic: xFormation
,kC] ,iC] ,jC] ,C]
,kT] ,iT] ,jT] ,T]
As I have noted everything has a context. So it would be useful to have a formalism that denotes Contexts as part of the formalism.